Критерии распознавания открытого текста

Заменив реальный открытый текст его моделью, мы можем теперь построить критерий распознавания открытого текста. При этом можно воспользоваться либо стандартными методами различения статистических гипотез, либо наличием в открытых текстах некоторых запретов, таких, например, как биграмма ЪЪ в русском тексте. Проиллюстрируем первый подход при распознавании позначной модели открытого текста.

Итак, согласно нашей договоренности, открытый текст представляет собой реализацию независимых испытаний случайной величины, значениями которой являются буквы алфавита , появляющиеся в соответствии с распределением вероятностей . Требуется определить, является ли случайная последовательность букв алфавита открытым текстом или нет.

Пусть — гипотеза, состоящая в том, что данная последовательность — открытый текст, — альтернативная гипотеза. В простейшем случае последовательность можно рассматривать при гипотезе как случайную и равновероятную. Эта альтернатива отвечает субъективному представлению о том, что при расшифровании криптограммы с помощью ложного ключа получается “бессмысленная” последовательность знаков. В более общем случае можно считать, что при гипотезе последовательность представляет собой реализацию независимых испытаний некоторой случайной величины, значениями которой являются буквы алфавита , появляющиеся в соответствии с распределением вероятностей . При таких договоренностях можно применить, например, наиболее мощный критерий различения двух простых гипотез, который дает лемма Неймана — Пирсона ([Кра75]).

В силу своего вероятностного характера такой критерий может совершать ошибки двух родов. Критерий может принять открытый текст за случайный набор знаков. Такая ошибка обычно называется ошибкой первого рода, ее вероятность равна . Аналогично вводится ошибка второго рода и ее вероятность 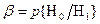. Эти ошибки определяют качество работы критерия. В криптографических исследованиях естественно минимизировать вероятность ошибки первого рода, чтобы не “пропустить” открытый текст. Лемма Неймана—Пирсона при заданной вероятности первого рода минимизирует также вероятность ошибки второго рода.

Критерии на открытый текст, использующие запретные сочетания знаков, например -граммы подряд идущих букв, будем называть критериями запретных -грамм. Они устроены чрезвычайно просто. Отбирается некоторое число редких -грамм, которые объявляются запретными. Теперь, просматривая последовательно -грамму за -граммой анализируемой последовательности , мы объявляем ее случайной, как только в ней встретится одна из запретных -грамм, и открытым текстом в противном случае. Такие критерии также могут совершать ошибки в принятии решения. В простейших случаях их можно рассчитать. Несмотря на свою простоту, критерии запретных -грамм являются весьма эффективными.

Шифр замены

Шифр замены, каждая очередная шифрвеличина при преобразовании заменяется некоторым своим образом - шифробозначением. История криптографии и шифров начинается более 2000 лет назад, когда Юлий Цезарь писал Цицерону, используя шифр, в котором каждая буква заменялась третьей последующей буквой латинского алфавита (с учетом циклического сдвига). Слово COMPUTER имело бы вид FRPSXWHU. Шифр Цезаря можно описать математически:

у = (х + k) mod 26, k = const,

где х,у - номера букв в латинском алфавите из 26 букв, каждая буква однозначно определяется своим номером от 0 до 25; k - ключ (число, задающее размер циклического сдвига). Сегодня раскрытие такого шифра делается легко. Здесь близкие буквы (в смысле соседства с учетом циклического сдвига) остаются близкими после шифрования, то есть сохраняется "расстояние" между открытым и шифрованным текстами, и каждая буква всегда заменяется на одну и ту же другую букву.

Усложнением шифра Цезаря является моноалфавитная подстановка (шифр простой замены). Здесь каждая буква текста заменяется другой буквой по фиксированному правилу. Ключом является матрица перестановки, содержащая единственную единицу в каждой строке и каждом столбце, остальные элементы - нулевые, и действующая на множестве букв входного алфавита. При этом шифр Цезаря является частным случаем моноалфавитной подстановки, ключевая матрица является матрицей сдвига.

Существенной характеристикой преобразования является вид отображения шифрвеличин на шифробозначение.

Возможно четыре случая:

1. Взаимоодназначные отображения, когда каждой шифрвеличине придается ровно одно шифробозначение и обратно, каждому шифробоз­начению соответствует только одна шифрвеличина. Шифры замены такого типа называются шифрами простой замены.

Криптоанализ моноалфавитных шифров осуществляется достаточно легко. Если известны открытый и соответствующий зашифрованный тексты, содержащие все буквы алфавита, то ключ вычисляется непосредственно. Если известны только зашифрованные тексты, то ключ вычисляется с помощью частотного анализа. Частотный анализ основан на том, что буквы алфавита появляются с различной частотой. Сравнивая частоту появления букв зашифрованного текста с частотой букв естественного языка, можно вычислить матрицу перестановки.

2. Шифры, неоднозначные по зашифрованию, если каждой шифрвели­чине соответствуют несколько шифробозначений, но любое шифробозначение скрывает за собой одну шифрвеличину. Если число шифробозначений, приданных шифрвеличине примерно пропорционально вероятности появления шифрвеличины в открытом тексте, то имеем так называемые пропорциональные шифры.

3. Известны случаи применения шифров, когда отдельные шифро­бозначения скрывают за собой одну из нескольких величин, то есть шифры неоднозначные по расшифрованию. При расшифровании нужная шифрвеличина подбирается по смыслу или с использованием дополни­тельных шифробозначений.

4. Наиболее сложный вид отображения - взаимонеоднознач­ное. Каждой шифрвеличине соответствует несколько шифробозначений и обратно, под данным шифробозначением могут скрываться различные шифрвеличины (в зависимости от ключевых установок) Почти всегда такие шифры можно рассматривать как некоторую комбинацию простых замен.

Большинство современных шифров строится именно по этому принципу.

Поиск по сайту: