 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Шифры и их классификация
Как показывает проведенный исторический экскурс, в качестве наиболее общего признака классификации шифров принят вид осуществляемых над шифрвеличинами преобразований – шифры перестановки и замены.
Принято различать криптоалгоритмы по степени доказуемости их безопасности. Существуют:
· безусловно стойкие (теоретически недешифруемые (ТНДШ));
· практически стойкие системы (для которых существует единственное правильное решение, но для его вычисления потребуется нереализуемо большое количество операций и(или) памяти (ПНДШ))
o доказуемо стойкие;
o предположительно стойкие криптоалгоритмы (практически недешифруемые).
Безопасность безусловно стойких криптоалгоритмов основана на доказанных теоремах о невозможности раскрытия ключа. Примером безусловно стойкого криптоалгоритма является система с разовым использованием ключей (шифр Вернама) или система квантовой криптографии, основанная на квантовомеханическом принципе неопределенности. Стойкость доказуемо стойких криптоалгоритмов определяется сложностью решения хорошо известной математической задачи, которую пытались решить многие математики и которая является общепризнанно сложной. Примером может служить система Диффи-Хеллмана или Ривеста-Шамира-Аделмана, основанные на сложностях соответственно дискретного логарифмирования и разложения целого числа на множители. Предположительно стойкие криптоалгоритмы основаны на сложности решения частной математической задачи, которая не сводится к хорошо известным задачам и которую пытались решить один или несколько человек. Примерами могут быть криптоалгоритмы ГОСТ 28147-89, DES, FEAL.
К сожалению, безусловно стойкие криптосистемы неудобны на практике (системы с разовым использованием ключа требуют большой защищенной памяти для хранения ключей, системы квантовой криптографии требуют волоконно-оптических каналов связи и являются дорогими, кроме того, доказательство их безопасности уходит из области математики в область физики).
Достоинством доказуемо стойких алгоритмов является хорошая изученность задач, положенных в их основу. Недостатком их является невозможность оперативной доработки криптоалгоритмов в случае появления такой необходимости, то есть жесткость этих криптоалгоритмов. Повышение стойкости может быть достигнуто увеличением размера математической задачи или ее заменой, что, как правило, влечет цепь изменений не только в шифровальной, но и в смежной аппаратуре.
Предположительно стойкие криптоалгоритмы характеризуются сравнительно малой изученностью математической задачи, но зато обладают большой гибкостью, что позволяет не отказываться от алгоритмов, в которых обнаружены слабые места, а проводить их доработку.
Кроме приведенной шкалы шифры могут классицированы по различным другим критериям, касающимся в основном способов реализации шифраторов, например:
· По размеру обрабатываемого (шифруемого) блока - блочные и поточные;
· По виду обрабатываемого сигнала – дискретные и аналоговые;
· По типу засекречиваемых сообщений – для засекречивания телеграфных, речевых, факсимильных сообщений или передачи данных
· По типу связи межу процессом шифрования и расшифрования – линейного и предварительного шифрования;
· По виду синхронизации между процессом шифрования и расшифрования- автономные, с каналом синхронизации и полуавтономные;
· …….
В качестве первичного признака, по которому производится классификация шифров, используется тип преобразования, осуществляемого с открытым текстом при шифровании. Если фрагменты открытого текста (отдельные буквы или группы букв) заменяются некоторыми их эквивалентами в шифртексте, то соответствующий шифр относится к классу шифров замены. Если буквы открытого текста при шифровании лишь меняются местами друг с другом, то мы имеем дело с шифром перестановки. С целью повышения надежности шифрования шифрованный текст, полученный применением некоторого шифра, может быть еще раз зашифрован с помощью другого шифра. Всевозможные такие композиции различных шифров приводят к третьему классу шифров, которые обычно называют композиционными шифрами. Заметим, что композиционный шифр может не входить ни в класс шифров замены, ни в класс шифров перестановки. В результате получаем первый уровень классификации шифров:
 |
Если ключ зашифрования совпадает с ключом расшифрования:  , то такие шифры называют симметричными, если же
, то такие шифры называют симметричными, если же  — асимметричными.
— асимметричными.
В связи с указанным различием в использовании ключей сделаем еще один шаг в классификации:
 |
Отметим также, что в приведенном определении правило зашифрования  является, вообще говоря, многозначной функцией. Выбор ее значений представляет собой некоторую проблему, которая делает многозначные функции
является, вообще говоря, многозначной функцией. Выбор ее значений представляет собой некоторую проблему, которая делает многозначные функции  не слишком удобными для использования. Избавиться от этой проблемы позволяет использование однозначных функций, что приводит к естественному разделению всех шифров замены на однозначные и многозначные замены (называемых также в литературе омофонами) (см. рис. 10).
не слишком удобными для использования. Избавиться от этой проблемы позволяет использование однозначных функций, что приводит к естественному разделению всех шифров замены на однозначные и многозначные замены (называемых также в литературе омофонами) (см. рис. 10).
Для однозначных шифров замены справедливо свойство:

для многозначных шифров замены:
 .
.
 |
Рис. 10
Исторически известный шифр пропорциональной замены представляет собой пример шифра многозначной замены, шифр гаммирования – пример шифра однозначной замены. Далее мы будем заниматься в основном изучением однозначных замен, получивших наибольшее практическое применение. Итак, далее  и
и  .
.
Заметим, что правило зашифрования  естественным образом индуцирует отображение
естественным образом индуцирует отображение 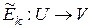 , которое в свою очередь продолжается до отображения
, которое в свою очередь продолжается до отображения  . Для упрощения записи будем использовать одно обозначение
. Для упрощения записи будем использовать одно обозначение  для каждого из трех указанных отображений.
для каждого из трех указанных отображений.
В силу инъективности (по  ) отображения
) отображения  и того, что
и того, что  , введенные в общем случае отображения
, введенные в общем случае отображения 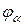 являются биекциями
являются биекциями  , определенными равенствами
, определенными равенствами  ,
, 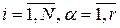 . Число таких биекций не превосходит
. Число таких биекций не превосходит  .
.
Для шифра однозначной замены определение правила зашифрования можно уточнить: в формуле (2) включение следует заменить равенством
 (2')
(2')
Введем еще ряд определений.
Если для некоторого числа 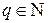 выполняются включения
выполняются включения  , то соответствующий шифр замены будем называть шифром равнозначной замены. В противном случае – шифром разнозначной замены:
, то соответствующий шифр замены будем называть шифром равнозначной замены. В противном случае – шифром разнозначной замены:
 |
В подавляющем большинстве случаев используются шифры замены, для которых  , для некоторого
, для некоторого 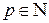 . При
. При  говорят о поточных шифрах замены, при
говорят о поточных шифрах замены, при  — о блочных шифрах замены:
— о блочных шифрах замены:
 |
Следующее определение. В случае  шифр замены называют одноалфавитным шифром замены или шифром простой замены. В противном случае – многоалфавитным шифром замены:
шифр замены называют одноалфавитным шифром замены или шифром простой замены. В противном случае – многоалфавитным шифром замены:
 |
Ограничиваясь наиболее важными классами шифров замены и исторически известными классами шифров перестановки, сведем результаты классификации в схему, изображенную на рис. 14.
Прокомментируем приведенную схему. Подчеркнем, что стрелки, выходящие из любого прямоугольника схемы, указывают лишь на наиболее значимые частные подклассы шифров. Пунктирные стрелки, ведущие из подклассов шифров перестановки, означают, что эти шифры можно рассматривать и как блочные шифры замены в соответствии с тем, что открытый текст делится при шифровании на блоки фиксированной длины, в каждом из которых производится некоторая перестановка букв. Одноалфавитные и многоалфавитные шифры могут быть как поточными, так и блочными. В то же время шифры гаммирования, образующие подкласс многоалфавитных шифров, относятся к поточным, а не к блочным шифрам. Кроме того, они являются симметричными, а не асимметричными шифрами.
Далее мы рассмотрим свойства большинства из указанных на схеме классов шифров.
 |
Рис. 14
Модели шифров
В любую систему шифрования (засекречивания) входят три объекта:
1. множество исходных сообщений { xi }, с распределением вероятностей { p(xi) }, i = 1,AL;
где – AL – множество декартовых степеней сообщений длины L составленных из элементов алфавита А.
2. множество ключей шифра { kj } с распределением вероятностей { p (kj)}, j = 1,S;
3. множество криптограмм { yj }, порождаемых взаимодействием случайно выбранного сообщения и ключей.
Описать систему шифрования (СШ) - это значит дать закон определяющий взаимно однозначное соответствие между открытым и шифрованным сообщениями. Такое описание может быть сделано аналитически с помощью функций, определяющих систему преобразований:
yi = f(xi,ki) - шифрование (засекречивание)
xi = d(yj, kj) - расшифрование (рассекречивание).
Например, такой функцией может быть булева функция неравнозначности, (сложения по модулю 2), Yi = Xi Å Ki Xi = Yi Å Kj
Заметим, если Ki шифрования и Kj расшифрования удовлетворяют Ki = Kj,то система называется симметричной.
В операторной форме Y i = X i * Q i - шифрование, X i = Y i * Q i-1 - расшифрование.
С помощью таблицы соответствия между парами xi, ki и шифрованными сообщениями yi:
Таблица 1
| Q1 | x1 | x2 | x3 |
| k1 | |||
| k2 | |||
| k3 |
Графически с помощью конечного графа, состоящего из двух колонок точек Ошибка! Источник ссылки не найден.. Каждой точке левой колонки соответствует открытое сообщение, каждой точке правой колонки соответствует одна из криптограмм.
Точка левой колонки соединяется с точкой правой колонки, если существует ключ, при котором соответствующее открытое сообщение преобразуется в соответствующую криптограмму. 
Используя графическое представление СШ введем некоторые понятия:
Система называется единственно шифруемой, если из каждой точки левой колонки выходят линии с разными ключами.
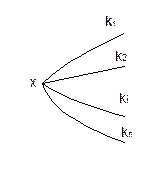

Система называется единственно расшифровываемой, если из каждой точки правой колонки выходят линии с разными ключами.
Если одно и то же сообщение может быть преобразовано в криптограмму разными ключами, то такие ключи называются эквивалентными см. x1 k¢11 и k11. В СШ со строго неэквивалентными ключами не может быть параллельных ребер, т.е. точки соединяются только одним ребром.
Остановимся более подробно на алгебраической модели шифров.
Пусть  — конечные множества возможных открытых текстов, ключей и шифрованных текстов соответственно;
— конечные множества возможных открытых текстов, ключей и шифрованных текстов соответственно; 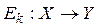 — правило зашифрования на ключе
— правило зашифрования на ключе  . Множество
. Множество  обозначим через
обозначим через  , а множество
, а множество  — через
— через 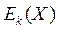 . Пусть
. Пусть 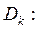
 — правило расшифрования на ключе
— правило расшифрования на ключе 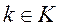 , и
, и  — это множество
— это множество 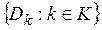 .
.
Здесь и далее мы будем предполагать, что если  представляется в виде
представляется в виде  , где
, где 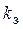 — ключ зашифрования, а
— ключ зашифрования, а  — ключ расшифрования (причем
— ключ расшифрования (причем 

 ), то
), то 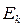 понимается как функция
понимается как функция 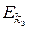 , а
, а  — как функция
— как функция  .
.
Определение 1. Шифром (шифрсистемой) назовем совокупность 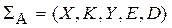 введенных множеств, для которых выполняются следующие свойства:
введенных множеств, для которых выполняются следующие свойства:
1) для любых  и
и  выполняется равенство
выполняется равенство
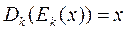 ;
;
2)  .
.
Неформально, шифр — это совокупность множеств возможных открытых текстов (то, что шифруется), возможных ключей (то, с помощью чего шифруется), возможных шифртекстов (то, во что шифруется), правил зашифрования и правил расшифрования.
Отметим, что условие 1) отвечает требованию однозначности расшифрования. Условие 2) означает, что любой элемент  может быть представлен в виде
может быть представлен в виде  для подходящих элементов
для подходящих элементов 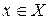 и
и 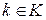 . Отметим также, что в общем случае утверждение “для любых
. Отметим также, что в общем случае утверждение “для любых 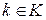 и
и  выполняется равенство
выполняется равенство  ” является неверным.
” является неверным.
Легко проверить, что из условия 1) следует свойство инъективности функции  . Другими словами, если
. Другими словами, если  , причем
, причем  , то при любом
, то при любом 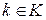 выполняется неравенство
выполняется неравенство  .
.
По сути дела определение 1 вводит математическую модель, отражающую основные свойства реальных шифров. В силу этого мы будем отождествлять реальный шифр с его моделью  , которую будем назвать алгебраической моделью шифра. Для подавляющего большинства известных шифров несложно составить такую модель, как это будет видно из дальнейшего.
, которую будем назвать алгебраической моделью шифра. Для подавляющего большинства известных шифров несложно составить такую модель, как это будет видно из дальнейшего.
Введем теперь вероятностную модель шифра. Следуя К.Шеннону, определим априорные распределения вероятностей  на множествах
на множествах  и
и  соответственно. Тем самым для любого
соответственно. Тем самым для любого  определена вероятность
определена вероятность 
 и для любого
и для любого  — вероятность
— вероятность 
 , причем выполняются равенства
, причем выполняются равенства

 и
и 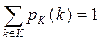 .
.
В тех случаях, когда нам требуется знание распределений  и
и 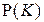 , мы будем пользоваться вероятностной моделью
, мы будем пользоваться вероятностной моделью  , состоящей из пяти множеств, связанных условиями 1) и 2) определения 1, и двух вероятностных распределений:
, состоящей из пяти множеств, связанных условиями 1) и 2) определения 1, и двух вероятностных распределений:  = (
= ( ).
).
Забегая вперед, отметим, что вероятностные характеристики шифров используются лишь в криптоанализе — разделе криптографии, посвященном решению задач вскрытия (или взлома) шифров.
В большинстве случаев множества 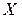 и
и  представляют собой объединения декартовых степеней некоторых множеств
представляют собой объединения декартовых степеней некоторых множеств  и
и  соответственно, так что для некоторых натуральных
соответственно, так что для некоторых натуральных  и
и 
 .
.
Множества  и
и  называют соответственно алфавитом открытого текста и алфавитом шифрованного текста. Другими словами, открытые и шифрованные тексты записываются привычным образом в виде последовательностей букв.
называют соответственно алфавитом открытого текста и алфавитом шифрованного текста. Другими словами, открытые и шифрованные тексты записываются привычным образом в виде последовательностей букв.
Поиск по сайту: