 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод простых итераций
Пусть уравнение (2.1) можно заменить эквивалентным ему уравнением
x = j (x). (2.4)
Например, уравнение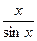 
– 0.5 = 0 можно заменить эквивалентным ему уравнением x = 0.5sin x.
Выберем каким-либо образом начальное приближение x 0. Вычислим значение функции j (x) при x = x 0 и найдем уточненное значение x 1 = j (x 0). Подставим теперь x 1 в уравнение (2.4) и получим новое приближение x 2 = j (x 1) и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню:
x n+1 = j (xn). (2.5)
Формула (2.5) является расчетной формулой метода простых итераций.
Если последовательность { x n} сходится при n® 
, т. е. существует
x* =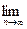 
xn, (2.6)
и функция j (x) непрерывна, то, переходя к пределу в (2.5) и учитывая (2.6), получим:
x* = 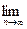xn = 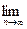j (x n - 1) = j ( 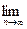xn - 1) = j (x*).
Таким образом, x * = j (x*), следовательно, x * – корень уравнения (2.4).
Сходимость метода. Сходимость метода простых итераций устанавливает следующая теорема.
Теорема 2.2. Если в интервале, содержащем корень x* уравнения (2.4), а также его последовательные приближения x 0, x 1, …, x n, …, вычисляемые по формуле (2.5), выполнено условие:
| j' (x)| £ q < 1, (2.7)
то x* = 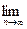xn.
т. е. итерационный процесс сходится и справедлива следующая оценка погрешности:
| xn – x* | £ qn | x 0 – x* | (2.8)
Оценка (2.8) является априорной. Она показывает, что метод простой итерации сходится со скоростью геометрической прогрессии с знаменателем q. Чем меньше q, тем выше скорость сходимости.
Как следует из теоремы 2.2, условие (2.7) является достаточным для сходимости метода простых итераций. Его выполнение гарантирует сходимость процесса (2.5), но невыполнение условия (2.7), вообще говоря, не означает, что итерационный процесс будет расходиться.
Погрешность метода. Если известна величина q в условии (2.7), то применима следующая апостериорная оценка погрешности:
| xn – x* | £ 
| xn – xn – 1|, n > 1. (2.9)
Критерий окончания. Из оценки (2.9) вытекает следующий критерий окончания итерационного процесса. Вычисления следует продолжать до выполнения неравенства
| xn – xn – 1| <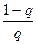 
e.
Если это условие выполнено, то можно считать, что xn является приближением к x* с точностью e.
Если q £ 0.5, то можно пользоваться более простым критерием окончания:
| xn – xn – 1| < e. (2.10)
Решение нелинейных уравнений методом простых итераций
Контрольный пример. Найти один действительный корень уравнения x = 0.5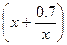 
с точностью e = 10-5.
Код программы:
| Program metod_prostyh_iteraciy; uses crt; var x1,x0,eps:real; i:integer; function f(x:real):real; {описание функции } begin f:=2*x-cos(x) end; {описание функции для интеграционного уравнения x=fi(x)} function fi(x:real):real; begin fi:=0.5*(x-0.7/x); end; {Описание метода итераций } function iterac(var x0,e:real):real; var n:integer;delta,j:real; begin j:=(-1); n:=0; writeln(промежуточные значения итерация); repeat delta:=abs(x0-fi(x0)); write('x', n:1, ' = ',x0:8:5,' fi(x',n:1, ')=', fi(x0):8:5,' eps=',delta:8:5); x0:=fi(x0); n:=n+1; readln; until (delta<e) or (n>300); writeln('число интераций =',n); iterac:= x0 end; begin clrscr; write(начальное значение корня= ');readln(x0); write(Точность вычисления= ');readln(eps); x1:=iterac(x0,eps); writeln(приближенное значение корня',eps:7:5); writeln('x = ',x1:8:6); readln end. |
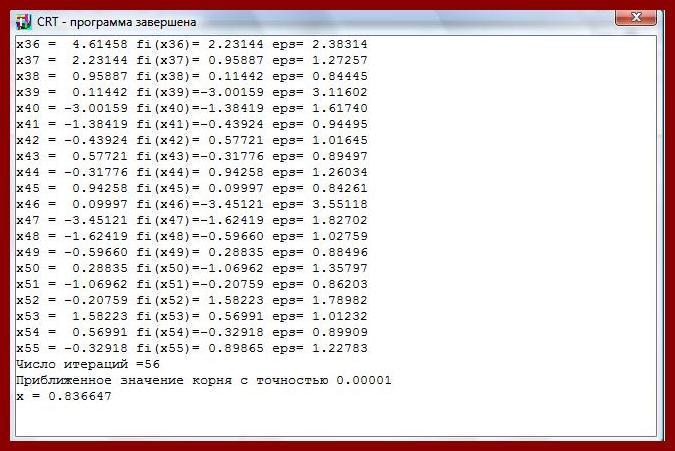
Проверка:
(0.5*(0.8366-0.7/0.8366))=-0,00006
Поиск по сайту: