Уравнения Хартри-Фока для замкнутых оболочек

Прежде всего, стоит пояснить, какие оболочки считаются замкнутыми. С этим связано понятие спаренные электроны.

Два электрона системы, различающиеся в одноэлектронном приближении только своим спинами, называются спаренными.

В свою очередь, система, состоящая из спаренных электронов, называется системой с замкнутыми оболочками.

Большинство молекул, находящиеся в основном состоянии, представляют собой системы с замкнутыми оболочками (хотя есть и исключения, например молекула О₂, основное состояние которой триплет, то есть ее спин равен 1).

Все системы с нечетным числом электронов являются системами с незамкнутыми оболочками (или открытыми оболочками).

Такими же являются системы со спином, отличным от нуля. Системы с открытыми оболочками обладают одной особенностью. Их волновые функции могут не быть собственными функциями оператора 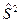, что не очень приемлемо с физической точки зрения. И, как следствие этого, волновые функции системы с незамкнутыми оболочками лишь в особых случаях можно представить в виде одного слейтеровского детерминанта (дальше будем говорить просто детерминанта). В квантовой химии волновые функции в виде одного детерминанта называются однодетерминантными, волновые функции в виде нескольких детерминантов – многодетерминантными волновыми функциями. Итак, поскольку волновые функции системы с замкнутыми оболочками могут быть представлены однодетерминантой волновой функцией, их описание гораздо проще. Рассмотрим систему с замкнутой оболочкой, в которой имеется N=2n электронов. Пробная функция может быть представлена в виде

(III.64)

Черта над спин-орбиталью означает, что ей отвечает противоположный спин. Например, если 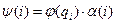, то , где 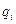– набор пространственных координат электронов. Уравнения Хартри-Фока для такой системы будут:

Причины суммирования до n, а не до 2n, и наличие двойки в кулоновском члене, как и ее отсутствие в обменном члене, прояснится дальше при рассмотрении выражения для полной энергии такой системы.

Как мы уже говорили ε_к являются орбитальными энергиями. Выясним более полно физический смысл ε_к. Энергия такой системы, как мы видели раньше,

(III.66)

Проинтегрируем выражение (III.66) по спинам в предположении, что спин -орбитали являются произведением пространственной и спиновой функций. Получим следующее выражение для энергии:

где

(III.68)

Прокомментируем наличие четырех комбинаций спиновых функций в кулоновском интеграле и только двух – в обменном. В кулоновском интеграле каждый электрон находится на одной орбитали и поэтому в этом случае возможны четыре различные комбинации: оба электрона имеют одинаковые спины (либо оба имеют спин α, либо оба – β), либо они имеют разные спины (первый имеет спин α, а второй имеет спин β, либо наоборот). В обменном интеграле электроны распределены по обеим орбиталям и поэтому возможны только две комбинации. Например, пусть электрон с условным номером 1 на орбитали φ* _i имеет спин α. Тогда на орбитали φ _j этот электрон тоже имеет спин α, поскольку это один и тот же электрон. А электрон с номером два на двух других орбиталях может по принципу Паули иметь только спин β. Вторая возможная комбинация соответствует спинам, противоположным первой комбинации. Никакая третья комбинация спинов здесь невозможна без нарушения принципа Паули. В чем можно легко убедиться, следуя приведенным логическим рассуждениям. Эти рассуждения проясняют и вид выражения (III.65). Итак, энергия системы с замкнутыми оболочками имеет вид:

(III.69)

Удалим теперь из системы один электрон в состоянии с каким-нибудь определенным спином.

, (III.70)

где означает или .

Энергия такой системы является разностью между энергией системы, содержащей 2n электронов и вкладом в эту энергию электрона в состоянии . Нетрудно показать, что разность между энергиями системы с 2n электронами и 2n-1 электроном равна

(III.71)

Эта разность представляет собой (с обратным знаком) величину энергии ионизации электрона из состояния .

С другой стороны, если уравнение (III.65) умножить на и проинтегрировать по всему пространству, то получим выражение для орбитальной энергии:

(III.72)

Сравнивая (III.71) и (III.72), видим, что , то есть - есть энергия ионизации из системы электрона, находящегося в состоянии . В этом и заключается теорема Купменса. Чаще ее произносят так :