Частица в одномерном потенциальном ящике

Рассмотрим движение частицы вдоль оси Ох в интервале x ≥ 0 и x ≤ a, таком, что внутри него потенциальная энергия равна нулю (U=0), а за его границами она бесконечно велика (U→∞). Такая система называется одномерным потенциальным ящиком (ямой). В этом случае ситуация аналогична движению свободной частицы, за исключением граничных условий. Потенциальный ящик показан на Рис. 5.

Поэтому стационарное уравнение Шредингера будет:

(II.80)

или

(II.81)

Рис.5. Схематическое изображение одномерного потенциального ящика.

Из определения потенциального ящика следует, что должны выполняться следующие граничные условия:

(II.82)

(II.83)

Вне ящика частица находиться не может, так как для этого ей надо сообщить бесконечно большую энергию.

Из теории линейных дифференциальных уравнений 2^го порядка известно, что общее решение уравнения вида (II.81) надо искать в виде:

Оно действительно удовлетворяет уравнению типа 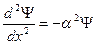, где для краткости обозначено

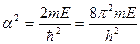(II.84)

Условие (II.82) выполняется, если B = 0. Условие (II.83) выполняется, если , где n=0,1,2,3,……… То есть

и

(II.85)

Сравнивая (II.84) и (II.85), получаем:

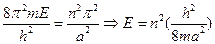(II.86)

Волновая функция должна быть нормированной, исходя из ее физического смысла, связанного с вероятностью обнаружения частицы в определенном месте пространства. Следующее равенство соответствует тому, что вероятность обнаружения частицы во всем пространстве является достоверным событием:

(II.87)

В рассматриваемом случае это требование приобретает вид:

(II.88)

Такие пределы интегрирования обусловлены тем, что за пределами ящика волновая функция равна нулю.

Вычисление А из (II.88) показывает, что: .

Таким образом:

(II.89)

и

(II.90)

То есть Е обратно пропорциональна m и a. Чем тяжелее частица и чем шире потенциальный ящик, тем ближе уровни энергии друг к другу. Например, при m = 1г и a = 1см они практически сливаются. Квантование имеет смысл при .

Поиск по сайту: