ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ

Важными динамическими характеристиками объекта являются его частотные характеристики, которые определяют взаимо­связь между параметрами периодических сигналов на входе и вы­ходе. Чаще всего их используют для описания одноканальных объ­ектов:

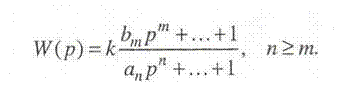Если на его вход подавать гармонический сигнал заданной ам­плитуды А₁ и частоты ω,

и = A₁cos ωt,

то на выходе в установившемся режиме у устойчивого объекта (гл. 4) будет также гармонический сигнал той же частоты, но в об­щем случае другой амплитуды со сдвигом по фазе

у = А₂cos(ωt + φ).

Для нахождения соотношения между входным и выходным гар­моническими сигналами можно воспользоваться передаточной функцией (2.38), из которой формальной заменой р на jω получим обобщенную частотную характеристику

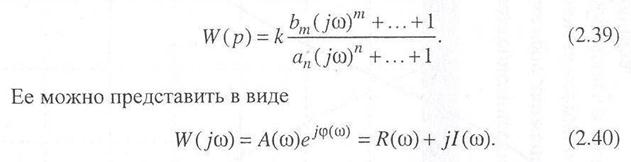Составляющие обобщенной частотной характеристики W(jω) имеют самостоятельное значение и следующие названия:

R(ω) - вещественная частотная характеристика (ВЧХ),

I(ω) - мнимая частотная характеристика (МЧХ),

A (ω) - амплитудная частотная характе­ристика (АЧХ),

φ(ω)- фазовая частотная характеристика (ФЧХ).

Для исследования частотных свойств объекта или системы удобно использовать графическое представление частотных харак­теристик. В этом случае обобщенная частотная характеристика W(jω) может быть построена на комплексной плоскости в соот­ветствии с выражением (2.40), когда каждому значению частоты ω₁, соответствует вектор W(jω_i).

При изменении ω от 0 до ∞ ко­нец этого вектора «прочерчи­вает» на комплексной плоско­сти кривую, которая называет­ся амплитудно-фазовой ха­рактеристикой (АФХ).

Наряду с амплитудно-фазо­вой характеристикой (рис. 2.8) можно также построить все остальные частотные характе­ристики. Так, амплитудная частотная характеристика по­казывает, как звено пропускает

Сигналы различной частоты; причем оценкой пропускания является отношение амплитуд выходного (А₂) и входного сигналов (А₁). Фазовая частотная характеристика отражает фазовые сдвиги, вносимые системой на различных частотах.

Наряду с рассмотренными частотными характеристиками в тео­рии автоматического управления используются логарифмические частотные характеристики. Удобство работы с ними объясня­ется тем, что операции умножения и деления заменяются на опера­циисложения и вычитания, а это позволяет во многих случаяхстроить их практически без вычислений.

Амплитудная частотная характеристика, построенная в лога­рифмическом масштабе,

L(w)=20 lg A(w)

называется логарифмической амплитудной частотной харак­теристикой (ЛАЧХ). При этом амплитуда измеряется в децибе­лах (дБ). При изображении ЛАЧХ (рис. 2.9) удобнее по оси абс­цисс откладывать частоту также в логарифмическом масштабе, т. е. lg ω, выраженную в декадах (дек.).

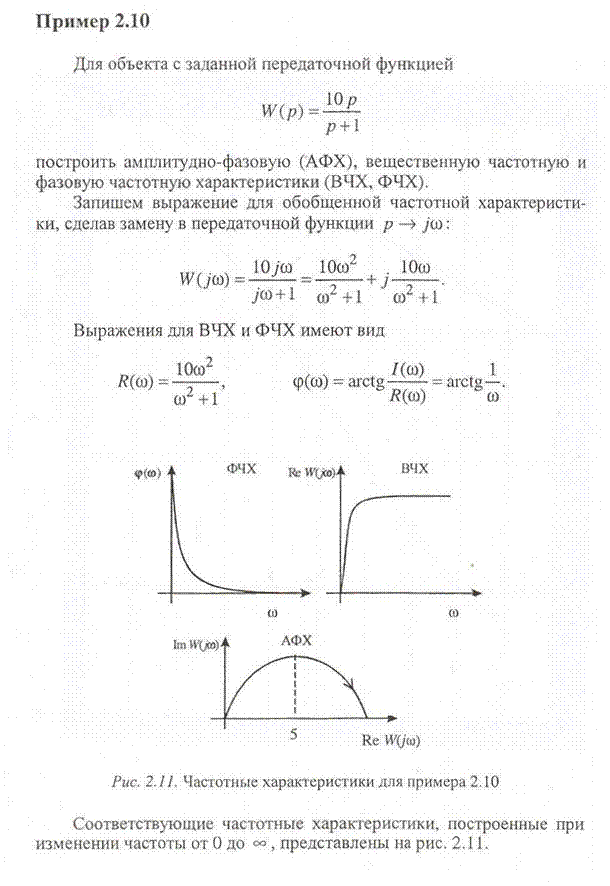
На практике применяется также и логарифмическая фазовая частотная характеристика. При ее изображении используется ось абсцисс, на которой указывают частоту в логарифмическом масштабе, а по оси ординат откладывают фазу в дуговых градусах в линейном масштабе (рис. 2.10).

ЗАКЛЮЧЕНИЕ

Этот раздел является в некотором смысле вводным для всех по­следующих. В нем приведены основные способы представления математических моделей, которые в дальнейшем будут использо­ваны для исследования свойств объектов и систем управления. По­нятно, что введенные здесь характеристики отражают их поведе­ние не только в динамике, но и в статике, поскольку статический режим представляет собой предел переходных процессов.

Наряду с динамическими характеристиками, которые исполь­зуются в классической теории управления (переходные характе­ристики, передаточные функции, частотные характеристики), здесь рассмотрены также модальные характеристики и приведено описа­ние объектов в переменных состояния, что соответствует совре­менной теории управления. Дальнейшее содержание не требует более широких сведений о характеристиках систем, хотя в научной литературе есть попытки их описания с использованием и других математических конструкций.

Обращаем внимание на то, что ни одна математическая модель не может абсолютно точно отражать свойства физической систе­мы, как бы ни повышали ее сложность с целью уточнения. Поэто­му обычно стремятся получить модель, которая достаточно адек­ватно отражает свойства физического устройства и не является слишком сложной. В дальнейшем, говоря об объекте или системе, будем иметь в виду их математическую модель, представленную одной из динамических характеристик.

ЛИТЕРАТУРА

1. Андреев Ю.Н. Управление конечномерными линейными объектами. - М.: Наука, 1978.

2. Беллман Р. Введение в теорию матриц. - М.: Наука, 1976.

3. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. - М.: Наука, 1974.

4. Гноенский Л.С, Каменский Г.С, Элъсгольц Н.Э. Математические основы теории управляемых систем. - М.: Наука, 1969.

5. Деруссо П.М. и др. Пространство состояний в теории управле­ния. - М.: Наука, 1970.

6. Ерофеев А. А. Теория автоматического управления. - СПб.: Политехника, 1998.

7. Заде Л., Дезоер Ч. Теория линейных систем. Метод пространства состояний. - М.: Наука, 1970.

8. Иванов В.А., Чемоданов В.К., Медведев B.C. Математические ос­новы теории автоматического регулирования. - М.: Высш. шк., 1973.

9. Квакернаак X., Сиван Р. Линейные оптимальные системы управ­ления. - М.: Мир, 1977.

10.Первозванский А.А. Курс теории автоматического управления. -М.: Высш. шк., 1986.

Поиск по сайту: