 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нескінченно малі та нескінченно великі функції
ЛЕКЦІЯ №13.
ТЕМА: «Нескінченно малі функції, їх властивості, визначні границі, односторонні границі.»
ПЛАН.
1. Нескінченно малі та нескінченно великі функції.
2. Визначні границі.
3. Односторонні границі.
4. Асимптоти функції.
ХІД ЛЕКЦІЇ:
Нескінченно малі та нескінченно великі функції.
Функція 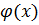 називається нескінченно малою для
називається нескінченно малою для 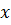 →𝑎, якщо
→𝑎, якщо 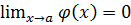 . Функція
. Функція  називається нескінченно великою для
називається нескінченно великою для 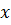 →𝑎, якщо
→𝑎, якщо 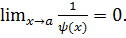
Нескінченно малі для 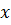 →𝑎 функції
→𝑎 функції 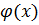 і
і 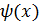 називаються еквівалентними, якщо
називаються еквівалентними, якщо 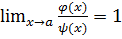 ; позначають:
; позначають:  .
.
Основні властивості нескінченно малих функцій:
| Властивість | Аналітичний запис |
Алгебраїчна сума двох (скінченної кількості) нескінченно малих функцій 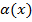 та та 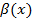 є нескінченно малою функцією. є нескінченно малою функцією.
| якщо 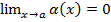 та та 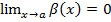 , то , то 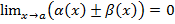
|
| Добуток обмеженої функції на нескінченно малу функцію є нескінченно малою функцією | якщо 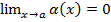 та та 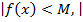 , то , то 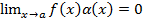
|
Якщо 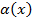 – нескінченно мала функція при – нескінченно мала функція при  , то , то 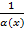 – нескінченно велика функція при – нескінченно велика функція при 
| якщо 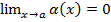 , то , то 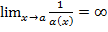
|
Основні властивості нескінченно великих функцій:
Поиск по сайту: