АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Способ подстановки (замены переменных)

Читайте также:
  1. I. Открытые способы определения поставщика.
  2. II. Решение логических задач табличным способом
  3. III. Глава о необычных способностях.
  4. III. Способы очистки.
  5. Абиотические факторы и приспособления к ним
  6. Абстрактное мышление – высокая способность к обучаемости.
  7. АДАПТАЦИЯ И ОСНОВНЫЕ СПОСОБЫ ПРИСПОСОБЛЕНИЯ ЖИВЫХ ОРГАНИЗМОВ К ЭКСТРЕМАЛЬНЫМ УСЛОВИЯМ СРЕДЫ
  8. Анализ и оценка реальных возможностей восстановления платежеспособности предприятия
  9. Анализ как способ развития экономического мышления
  10. Анализ конкурентоспособности продукции
  11. АНАЛИЗ КРЕДИТОСПОСОБНОСТИ КРЕДИТОПОЛУЧАТЕЛЯ
  12. Анализ ликвидности и платежеспособности

Теорема: Если требуется найти интеграл , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:

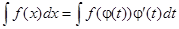
Пример. Найти неопределенный интеграл .

Сделаем замену t = sinx, dt = cosxdt.

Интегрирование по частям.

Способ основан на применении формулы интегрирования по частям ;

Пример.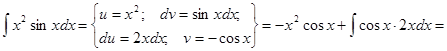

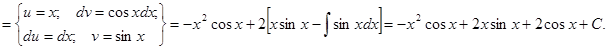
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

Вопросы для самоконтроля

1. Что такое первообразная функция?

2. Какими свойствами обладает неопределённый интеграл?

3. Чему равен неопределенный интеграл функции lnx?

4. В чем суть метода подстановки (замены переменной) в неопределенном интеграле?

5. В чем состоит метод неопределенных коэффициентов при интегрировании рациональныхдробей?


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)