 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Неопределенный интеграл
Интегральное исчисление
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Первообразная функция
Определение: Функция F(x) называется первообразной функциейфункции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл
Определение: Неопределенным интеграломфункции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 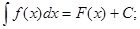
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1. 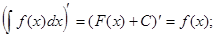
2. 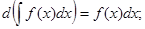
3. 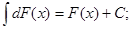
4.  где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
5. 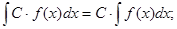
Таблица интегралов
Таблица 1 – Интегралы некоторых элементарных функций
| Интеграл | Значение | Интеграл | Значение | ||
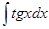
| -ln½cosx½+C | 
| ex + C | ||

| ln½sinx½+ C | 
| sinx + C | ||

| 
| 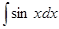
| -cosx + C | ||
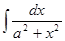
| 
| 
| tgx + C | ||

| 
| 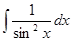
| -ctgx + C | ||

| ln 
| 
| arcsin 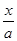 + C + C
| ||

| 
| 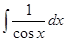
| 
| ||

| 
| 
| 
|
Поиск по сайту: