АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Критерии разнообразия признака в совокупности

Читайте также:
  1. B) наиболее часто встречающееся значение признака в данном ряду
  2. III.4. Критерии оценки преступления. Вина
  3. V. Вариационные ряды, средние величины, вариабельность признака
  4. Алгебраические критерии устойчивости
  5. Алгебраические критерии устойчивости
  6. База данных - это воплощенные на материальном носителе совокупности данных, подбор и расположение которых представляют результат творческого труда.
  7. Безопасность – понятие, опасность и риск, объекты, субъекты безопасности, критерии безопасности, виды безоп., системы безоп. и их характеристика
  8. Бронхиальная астма, клиника, критерии тяжести и оценка тяжести приступа
  9. Бронхиолит. Особенности клиники, критерии диагностики. Принципы лечения.
  10. В философии. Критерии истины
  11. Виды дисперсий в совокупности,разделенной на группы
  12. Виды посредников и их функции. Критерии выбора посредников

Величина того или иного признака неодинакова у всех единиц наблюдения совокупности, несмотря на ее относительную однородность. Например, уровень АД у отдельных лиц, страдающих артериальной гипертензией, неодинаков. В этом проявляется разнообразие (колеблемость) признака в изучаемой совокупности. Средняя арифметическая величина находится в большой зависимости от колеблемости вариационного ряда. Чем меньше колеблемость ряда (разность между самой большой и самой малой величиной), тем более точно его будет характеризовать средняя арифметическая.

Если большинство вариант концентрируется около своей средней арифметической величины, то такой вариационный ряд – довольно однородный. Если же варианта значительно удалена от своей средней арифметической – налицо большое варьирование, а возможно, и неоднородная совокупность.

Критериями, определяющими уровень разнообразия каждого признака в совокупности, являются: лимит (lim), амплитуда (Am), среднее квадратическое отклонение (d) и коэффициент вариации (CV).

Лимит (lim) определяется крайними значениями вариант в вариационном ряду: lim = Vmax ¸ Vmin

Амплитуда (Am) – разность крайних вариант.

 

Наиболее полную характеристику разнообразию признака дает среднее квадратическое отклонение – сигма (σ).

Для вычисления среднего квадратического отклонения (σ) необходимо определить отклонения (d) каждой варианты от средней, возвести их в квадрат (d2), перемножить квадрат отклонений на частоту каждой варианты (d2p), получить сумму этих произведений (å d2p), а затем вычислить σ по формуле:

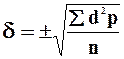
При малом числе наблюдений (n£30) расчет производится по формуле:

 

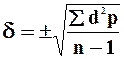
Для оценки варьирования признака в совокупности наряду со средним квадратическим отклонением может быть использован коэффициент вариации (CV). Особенно необходимо использовать коэффициент вариации для сравнения варьирования двух или более средних величин, выраженных в разных единицах измерения (сантиметрах, килограммах и др.):

Значение коэффициента вариации менее 10% свидетельствует о малой колеблемости, от 10 до 20% – о средней, больше 20% – о сильной колеблемости вариант вокруг средней.

Значение среднего квадратического отклонения – σ:

1. σ характеризует однородность вариационного ряда. Если σ мала, значит ряд однородный и рассчитанная М достаточно верно характеризует данный вариационный ряд. Если σ велика, то ряд неоднородный и полученная М характеризует не весь ряд, а какую-то ее часть.

2. Теоретическое распределение вариант в однородном ряду подчиняется правилу трех сигм:

М ± 1 σ = 68,3%

М ± 2 σ = 95,5%

М ± 3 σ = 99,7%.

В пределах М±1 σ находится 68,3% всех вариант (наблюдений), в пределах М±2 σ – 95,5%, а в пределах М±3 σ – 99,7% вариант, составляющих совокупность.

Если 95,5% всех вариант находится в пределах М±2 σ, то средняя арифметическая является характерной для данного ряда и не требуется увеличивать число наблюдений в совокупности. Для определения типичности средней арифметической сравнивают фактическое распределение с теоретическим путем расчета сигмальных отклонений.


1 | 2 | 3 | 4 | 5 | 6 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)