СРЕДНИЕ ВЕЛИЧИНЫ

Вариационный ряд - это ряд, в котором упорядоченно сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты. Отдельные числовые значения признака называются вариантами (V), а числа, показывающие, как часто эти варианты повторяются - частотами (Р), общее число наблюдений (n) равно сумме частот (n=SP, S - знак суммы).

Вариационный ряд может быть простым (при малом числе наблюдений –n£30) или сгруппированным (n>30); открытым и закрытым. По характеру распределения: альтернативным (имеет только 2 противоположных значения признака - да, нет), симметричным (наибольшее число наблюдений приходится на середину ряда) и ассиметричным (наибольшее число наблюдений сдвигается в сторону меньшего значения признака - правосторонняя ассиметрия, или в сторону большего значения признака - левосторонняя ассиметрия, или же скапливается по концам ряда - бимодальное распределение).

Построение вариационного ряда из отдельных вариант – это только первый шаг к осмыслению особенностей всей совокупности. Далее необходимо определить средний уровень изучаемого количественного признака.

Средняя величина – это число, выражающее общую меру исследуемого признака в совокупности.

Различают несколько видов средних величин: мода (Мо), медиана (Ме) и средняя арифметическая (М).

Мода (Мо) - наиболее часто повторяющаяся варианта, т.е. та, которой соответствует наибольшее количество частот (Р) вариационного ряда.

Медиана (Ме) - варианта, занимающая срединное положение в вариационном ряду. При нечетном числе наблюдений для определения медианы надо найти середину ряда – медианой будет центральная (срединная) варианта. При четном числе наблюдений за медиану принимают среднюю величину из двух центральных вариант.

Наиболее часто используется средняя арифметическая величина (М). Она имеет 3 основных свойства:

1. Занимает срединное положение в вариационном ряду. В строго симметричном ряду М = Мо = Ме;

2. Имеет абстрактный характер и является обобщающей величиной, вскрывающей то типичное, что характерно для всей совокупности.

3. Алгебраическая сумма отклонений всех вариант от средней равна нулю. Если сумма отклонений вариант от средней равна нулю, то средняя вычислена правильно. На этом свойстве основан расчет средней по способу моментов.

Средняя арифметическая, которая рассчитана в вариационном ряду, где каждая варианта встречается только один раз (для всех вариант р=1), называется средней арифметической простой. Она определяется по формуле:

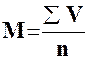где V – значение вариационного признака,

n – общее число наблюдений

Если в исследуемом ряду отдельные варианты встречаются различное число раз (р³1), то вычисляют среднюю арифметическую взвешенную. Расчет ее производится по формуле:

где Р – частота, n – сумма частот (å P).

Поиск по сайту: