АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Методы нахождения корней системы нелинейных уравнений

Читайте также:
  1. I. Формирование системы военной психологии в России.
  2. II. Методы непрямого остеосинтеза.
  3. II. Цель и задачи государственной политики в области развития инновационной системы
  4. II. Экономические институты и системы
  5. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  6. IV. Современные методы синтеза неорганических материалов с заданной структурой
  7. SCADA-системы
  8. SCАDA-системы: основные блоки. Архивирование в SCADA-системах. Архитектура системы архивирования.
  9. TRACE MODE 6: компоненты инструментальной системы
  10. А). Системы разомкнутые, замкнутые и комбинированные.
  11. А. И. Герцен – основатель системы вольной русской прессы в эмиграции. Литературно-публицистическое мастерство
  12. А. Механические методы

Для уточнения корней систем нелинейных уравнений наиболее часто используют методы итерации, Зейделя и метод Ньютона. Как и в случае уточнения корней одного нелинейного уравнения для систем требуется определение хорошего начального приближения (отделение корня), гарантирующего сходимость метода и высокую скорость сходимости. Для системы из 2 уравнений это можно сделать графически, но для систем высоких порядков удовлетворительных методов отделения корней не существует.

Дана система n нелинейных уравнений с n неизвестными:

,

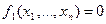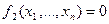, (1)

.

.

.

,

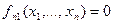Где , - нелинейные функции, определенные и не­прерывные в некоторой области 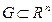, или в векторном виде:

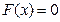(2)

где , .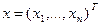

Требуется найти такой вектор 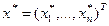, который при подстановке в систему (1) превращает каждое уравнение в векторное числовое равенство.

Замечание.

Проблема решения системы (1) возникает при решении многих при­кладных задач, например, поиска безусловного экстремума функций многих переменных с помощью необходимых условий [23], при применении неявных методов интегрирования обыкновенных дифференциальных уравнений [28] и т.д.

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)