Метод Ньютона

Основная идея метода Ньютона — решение системы нелинейных уравнений сводится к решению последовательности ли­нейных задач, дающих в пределе решение исходной задачи. Линейная задача получается путем выделения из нелинейных урав­нений главной линейной части.

Рассмотрим погрешность вычисления корня на k-ой итерации , где . Полагая, что функции f_i непрерывны и дифференцируемы в окрестности корня и - малые величины, разложим в ряд Тейлора, сохранив лишь линейную часть разложения. Получим систему уравнений:

, i=1,…,n (8)

Линейную относительно компонент вектора погрешностей. Если использовать эту систему для отыскания компонент вектора погрешностей, то в силу приближенности системы (8) – оставлена, лишь линейная часть – найденное значение вектора погрешности будет лишь приближенным. Тогда при подстановке полученного решения в соотношение будем иметь вместо x^* приближенное уточненное значение корня, которое обозначим через x^(k+1). Используя запись системы (8) в виде:

Где J(x) – матрица производных системы функций f_i(x) (матрицы Якоби), можем записать итерационный процесс для нахождения вектора x:

, k=0,1,…, (9)

Где

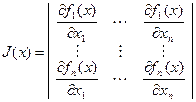- матрица Якоби

Так как процесс вычисления обратной матрицы является трудоемким, преобразуем (9) следующим образом:

, k=0,1,…

Где - поправка к текущему приближению x^(k)

Умножим последнее выражение слева на матрицу Якоби W(x^(k)):

, k=0,1,…

В результате получена система линейных алгебраических уравнений относительно поправки :

(10)

3. Вычислить следующее приближение:

(11)

4. Если , процесс закончить и положить . Если , то положить и перейти к пункту 2

Итерационный процесс метода Ньютона сходится, если определитель матрицы Якоби на k-й итерации J^(k)≠0. Требуется, однако, хорошее отделение корня, но достаточное условие сходимости слишком громоздко, чтобы им воспользоваться на практике.

2. К недостаткам метода Ньютона следует отнести:

- необходимость задавать достаточно хорошее начальное приближение;

- отсутствие глобальной сходимости для многих задач;

- необходимость вычисления матрицы Якоби на каждой итерации;

- необходимость решения на каждой итерации системы линейных уравне­ний, которая может быть плохо обусловленной.

Достоинством метода является квадратичная сходимость из хорошего начального приближения при условии невырожденности матрицы Якоби.

Пример 3.19. Решить систему:

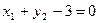
Методом Ньютона с точностью ε=0,001.

Очевидно, корнями системы являются ; . Найдем приближенно второй корень x_*2.

1. Зададим начальное приближение . В поставленной задаче ε=0,001. Положим k=0.

2. Составим систему (10). Так как , то система

имеет вид .

Для системы из двух уравнений поправку можно найти по формулам:

(11)

(12)

Отсюда . Для вычисления ∆x^(k), k=0,1,… здесь и далее используется метод Гаусса единственного деления.

3. Вычислим

4. Так как , то положим k=1 и перейдем к пункту 2.

5. Составим систему :

. Отсюда

6. Вычислим

7. Так как , то положим k=2 и перейдем к пункту 5. Результаты дальнейших вычислений приведены в таблице 3.19.

k
		-0,625	-0,091911	-0,002653	-0,0000023	0,0000
		3,625	3,091911	3,002653	3,0000023	3,0000
∆(k+1)	-	1,625	0,5333	0,089258	0,0026507	0,0000023

Найденное приближенное решение . Из анализа решения приведенного в таблице 3.19, следует, что количество верных знаков на каждой итерации удваивается, что соответствует квадратичной сходимости.

Поиск по сайту: