АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод итераций Зейделя

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. Методические основы
  3. I. Предмет и метод теоретической экономики
  4. II. Метод упреждающего вписывания
  5. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  6. II. Методы непрямого остеосинтеза.
  7. II. Проблема источника и метода познания.
  8. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  9. III. Методологические основы истории
  10. III. Предмет, метод и функции философии.
  11. III. Социологический метод
  12. III. УЧЕБНО – МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО КУРСУ «ИСТОРИЯ ЗАРУБЕЖНОЙ ЛИТЕРАТУРЫ К. XIX – НАЧ. XX В.»

Нередко сходимость метода простой итерации можно улучшить, если вновь вычисленные значения компонент вектора неизвест­ных немедленно включить в расчет. В этом случае итерационный процесс имеет вид:

, i=1,…,n (7)

Сходимость этого процесса также линейная.

Условием окончания итераций, методами итерации и Зейделя является достижение заранее заданной точности ε.

Если

Пример 1.

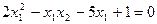
Расположенные в первом квадранте, методом простых итераций с точностью до ε=0,001.

Преобразуем систему к виду (3) так, чтобы выполнилось условие сходимости:

Найдем частные производные:

,

,

Здесь принято . Далее воспользуемся методикой решения задачи.

1. Для выбора начального приближения найдем координаты точек пересечения кривых, соответствующих первому и второму уравнениям.

(рис 3.17)

 

Находим приближенные значения координат решения (по условию задачи нас интересуют только корни с положительными координатами): .

Проверим выполнение условий сходимости. Будем рассматривать окрестность найденной точки 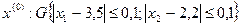. Тогда

;

 

;

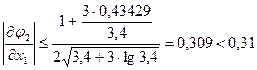Следовательно, можно получить оценки:

Очевидно, условие (5) выполняется. Если последовательные приближения не будут выходить из области G, то согласно теореме 3.13 итерационный процесс будет сходящимся. В поставленной задаче ε=0,001.

2,3 Выполним расчеты по формуле (4):

, k=0,1,…,

А результаты поместим в таблицу 3.17:

k          
3,500 3,4785 3,4837 3,4848 3,4957
3,500 2,2654 2,2589 2,26049 2,26082
∆(k+1) - 0,0654 0,0065 0,00159 0,0009

Заметим, что величина ∆(k+1) при увеличении номера итерации уменьшается, что характерно для любого сходящегося процесса. Найдено приближенное решение:

. При этом , .

 


1 | 2 | 3 | 4 |

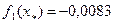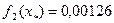Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.373 сек.)