АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод простых итераций

Читайте также:
  1. Aufgabe 2. Изучите образцы грамматического разбора простых предложений.Выберите из текста и разберите 3 простых предложения.
  2. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  3. I. Методические основы
  4. I. Предмет и метод теоретической экономики
  5. II. Метод упреждающего вписывания
  6. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  7. II. Методы непрямого остеосинтеза.
  8. II. Проблема источника и метода познания.
  9. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ
  10. III. Методологические основы истории
  11. III. Предмет, метод и функции философии.
  12. III. Социологический метод

В методе простой итерации система (1) приводится к эквивалентной системе вида , где , или

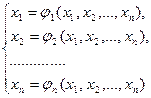(3)

Полагая известным начальное приближение для корня , построим итерационный процесс , k=0,1,2,…, или

(4)

в методе простой итерации вектор по­грешности испытывает линейное преобразование, или, иначе, метод имеет первый порядок сходимости.

Теорема 3.13 (о достаточном условии сходимости метода простых итераций).

Пусть функции и , i=1,…,n, непрерывны в области G, причем выполнено неравенство:

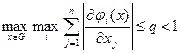, (5)

где q –некоторая постоянная.

Если последовательные приближения , k=0,1,… не выходят из области G, то процесс последовательных приближений сходятся и вектор x* является в области G единственным решением системы (3).

Замечание.

Вместо условия (5) можно также использовать:

(6)

 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)