Дисперсия света

Дисперсия света - это зависимость показателя преломления n вещества от длины волны света (в вакууме)   (4.12)

или, что то же самое, зависимость фазовой скорости световых волн от частоты:

(4.13)

Дисперсия вещества- это n производная по l   (4.14)

Для всех прозрачных бесцветных веществ в видимой части спектра с уменьшением длины волны показатель преломления увеличивается, то есть дисперсия вещества отрицательна: D<0. (рис. 4.7, области 1-2, 3-4)

Нормальная дисперсия вещества- это отрицательная дисперсия

Если вещество поглощает свет в каком-то диапазоне длин волн (частот), то в области поглощения дисперсия

оказывается положительной и называется аномальной (рис. 4.7, область 2-3).

Рис. 4.7. Зависимость показателя преломления (сплошная кривая) и коэффициента поглощения света веществом (штриховая кривая) от длины волны l вблизи одной из полос поглощения (l=l_0k)

Изучением нормальной дисперсии занимался Ньютон. Разложение белого света в спектр при прохождении сквозь призму является следствием дисперсии света. При прохождении пучка белого света через стеклянную призму на экране возникает разноцветный спектр (рис. 4.8).

Рис. 4.8. Прохождение белого света через призму: вследствие различия значений показателя преломления стекла для разных длин волн пучок разлагается на монохроматические составляющие — на экране возникает спектр

Наибольшую длину волны и наименьший показатель преломления имеет красный свет, поэтому красные лучи отклоняются призмой меньше других. Рядом с ними будут лучи оранжевого, потом желтого, зеленого, голубого, синего и, наконец, фиолетового света. Произошло разложение падающего на призму сложного белого света на монохроматические составляющие (спектр).

Ярким примером дисперсии является радуга. Радуга наблюдается, если солнце находится за спиной наблюдателя. Красные и фиолетовые лучи преломляются сферическими капельками воды и отражаются от их внутренней поверхности. Красные лучи преломляются меньше и попадают в глаз наблюдателя от капелек, находящихся на большей высоте. Поэтому верхняя полоса радуги всегда оказывается красной (рис. 26.8).

Рис. 4.9. Возникновение радуги

Используя законы отражения и преломления света, можно рассчитать ход световых лучей при полном отражении и дисперсии в дождевых каплях. Оказывается, что лучи рассеиваются с наибольшей интенсивностью в направлении, образующем угол около 42° с направлением солнечных лучей (рис. 4.10).

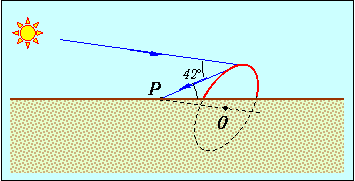
Рис. 4.10. Расположение радуги

Геометрическое место таких точек представляет собой окружность с центром в точке 0. Часть ее скрыта от наблюдателя Р под горизонтом, дуга над горизонтом и есть видимая радуга. Возможно также двойное отражение лучей в дождевых каплях, приводящее к радуге второго порядка, яркость которой, естественно, меньше яркости основной радуги. Для нее теория дает угол 51 °, то есть радуга второго порядка лежит вне основной. В ней порядок цветов заменен на обратный: внешняя дуга окрашена в фиолетовый цвет, а нижняя - в красный. Радуги третьего и высших порядков наблюдаются редко.

Элементарная теория дисперсии. Зависимость показателя преломления вещества от длины электромагнитной волны (частоты) объясняется на основе теории вынужденных колебаний. Строго говоря, движение электронов в атоме (молекуле) подчиняется законам квантовой механики. Однако для качественного понимания оптических явлений можно ограничиться представлением об электронах, связанных в атоме (молекуле) упругой силой. При отклонении от равновесного положения такие электроны начинают колебаться, постепенно теряя энергию на излучение электромагнитных волн или передавая свою энергию узлам решетки и нагревая вещество. В результате этого колебания будут затухающими.

При прохождении через вещество электромагнитная волна воздействует на каждый электрон с силой Лоренца:

(4.15)

где v - скорость колеблющегося электрона. В электромагнитной волне отношение напряженностей магнитного и электрического полей равно

(4.16)

Поэтому нетрудно оценить отношение электрической и магнитной сил, действующих на электрон:

(4.17)

Электроны в веществе движутся со скоростями, много меньшими скорости света в вакууме:

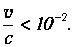
Таким образом, можно считать, что при прохождении через вещество электромагнитной волны на каждый электрон действует только электрическая сила:

(4.18)

где Е₀ - амплитуда напряженности электрического поля в световой волне, a - фаза, определяемая положением рассматриваемого электрона. Для упрощения вычислений пренебрежем затуханием и запишем уравнение движения электрона в виде

(4.19)

где. w₀ - собственная частота колебаний электрона в атоме. Решение такого дифференциального неоднородного уравнения мы уже рассматривали ранее и получили

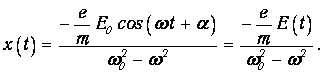
(4.20)

Следовательно, смещение электрона из положения равновесия пропорционально напряженности электрического поля. Смещениями ядер из положения равновесия в первом приближении можно пренебречь, так как массы ядер велики по сравнению с массой электрона.

Атом со смещенным электроном приобретает дипольный момент

(для простоты положим пока, что в атоме имеется только один «оптический» электрон, смещение которого вносит вклад в поляризацию). Если в единице объема содержится N атомов, то поляризацию среды (дипольный момент единицы объема) можно записать в виде

(4.21)

В реальных средах возможны разные типы колебаний зарядов (групп электронов или ионов), вносящих вклад в поляризацию. Эти типы колебаний могут иметь разные величины заряда е_i и массы т_i, а также различные собственные частоты w_0k (мы будем обозначать их индексом k), при этом число атомов в единице объема с данным типом колебаний N_k пропорционально концентрации атомов N:

Безразмерный коэффициент пропорциональности f_k обычно называют силой осциллятора. Сила осциллятора характеризует эффективный вклад каждого типа колебаний в общую величину поляризации среды:

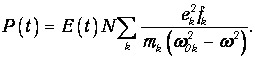
(4.22)

С другой стороны, как известно,

(4.23)

где c - диэлектрическая восприимчивость вещества, которая связана с диэлектрической проницаемостью e соотношением

В результате получаем выражение для квадрата показателя преломления вещества:

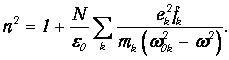
(4.24)

Вблизи каждой из собственных частот w_k функция n(w), определяемая формулой (4.24), терпит разрыв. Такое поведение показателя преломления обусловлено тем, что мы пренебрегли затуханием. Аналогично, как мы видели ранее, пренебрежение затуханием приводит к бесконечному росту амплитуды вынужденных колебаний при резонансе. Учет затухания избавляет нас от бесконечностей, и функция e=п² имеет вид, изображенный на рис. 4.11.

Рис. 4.11. Зависимость диэлектрической проницаемости среды e=n² от частоты электромагнитной волны

Учитывая связь частоты со с длиной электромагнитной волны в вакууме l

или

можно получить зависимость показателя преломления вещества п от длины волны в области нормальной дисперсии (участки 1-2 и 3-4 на рис. 4.7):

(4.25)

где

- длины волн, соответствующие собственным частотам колебаний w_0k, a_k - постоянные коэффициенты.

В области аномальной дисперсии (dn/dl>0) частота внешнего электромагнитного поля близка к одной из собственных частот колебаний молекулярных диполей, то есть возникает резонанс. Именно в этих областях (например, участок 2-3 на рис. 4.7) наблюдается существенное поглощение электромагнитных волн; коэффициент поглощения света веществом показан штриховой линией на рис. 4.7.

Понятие о групповой скорости. С явлением дисперсии тесно связано понятие о групповой скорости. При распространении в диспергирующей среде реальных электромагнитных импульсов, например известных нам цугов волн, испускаемых отдельными атомными излучателями, происходит их «расплывание» - расширение протяженности в пространстве и длительности во времени. Это связано с тем, что такие импульсы представляют собой не монохроматическую синусоидальную волну, а так называемый волновой пакет, или группу волн - совокупность гармонических составляющих с разными частотами w и с разными амплитудами, каждая из которых распространяется в среде со своей фазовой скоростью (4.13).

Если бы волновой пакет распространялся в вакууме, то его форма и пространственно-временная протяженность оставались бы неизменными, а скоростью распространения такого цуга волн была бы фазовая скорость света в вакууме

Из-за наличия дисперсии зависимость частоты электромагнитной волны от волнового числа k становится нелинейной, и скорость распространения цуга волн в среде, то есть скорость переноса энергии, определяется производной

где k₀ - волновое число для «центральной» волны в цуге (обладающей наибольшей амплитудой).

Мы не будем выводить эту формулу в общем виде, но на частном примере поясним ее физический смысл. В качестве модели волнового пакета примем сигнал, состоящий из двух плоских волн, распространяющихся в одном направлении с одинаковыми амплитудами А₀ и начальными фазами j₀=0, но различающихся частотами, сдвинутыми относительно «центральной» частоты w₀ на небольшую величину + Dw. Соответствующие волновые числа сдвинуты относительно «центрального» волнового числа k₀ на небольшую величину + Dk. Эти волны описываются выражениями:

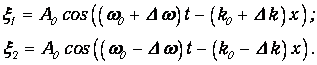
(4.26)

Для результирующей волны

после применения тригонометрической формулы для суммы двух косинусов получим выражение:

(4.27)

Мы убеждаемся, что результирующую волну можно представить как плоскую волну с «центральными» частотой w₀ и волновым числом k₀, амплитуда которой A(t) есть медленно меняющаяся (в силу малости сдвигов Dw<<w₀ и Dk<<k₀) функция времени и координаты. Похожий результат ранее был получен при изучении биений. Видно, что сама эта переменная амплитуда есть плоская волна, распространяющаяся со скоростью

В пределе бесконечно малых сдвигов частоты приходим к обсуждаемой формуле

(4.28)

Эта скорость называется групповой скоростью. Поскольку, как мы уже знаем, энергия колебаний определяется их амплитудой, «перемещение» последней и означает, что групповая скорость является скоростью переноса энергии волновым пакетом.

Фазовая же скорость волны есть отношение частоты к волновому числу:

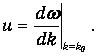
(4.29)

Дифференцируя это соотношение по k, находим связь фазовой и групповой скоростей:

(4.30)

Учитывая связь волнового числа с длиной волны

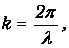
формулу (4.30) можно переписать в виде

(4.31)

Очевидно, что в отсутствие дисперсии

и групповая скорость не отличается от фазовой.

Групповая скорость как скорость распространения энергии в среде не может быть больше скорости света в вакууме, то есть всегда и<с, в то время как фазовая скорость света в среде не является предельной и может оказаться меньше скорости движения частиц в среде, например электронов. В этом случае, как мы уже знаем, возникает излучение Черенкова - Вавилова.

Расплывание волновых пакетов при их распространении в среде с дисперсией можно понять, если представить себе компактную группу из достаточно большого числа марафонцев, одновременно берущих старт, которая при приближении к финишу из-за разной скорости участников превратится в расплывшуюся в пространстве совокупность спортсменов, время прихода на финиш которых будет характеризовать временное расплывание этого аналога цуга волн. Таким образом, при перемещении в среде волнового пакета в целом с групповой скоростью происходит перемещение отдельных его волновых составляющих внутри пакета - ведь разные «участники» процесса движутся с разной «фазовой» скоростью.

Поиск по сайту: