Метод зон Френеля. Принцип Гюйгенса - Френеля в рамках волновой теории позволяет объяснить прямолинейное распространение света

Принцип Гюйгенса - Френеля в рамках волновой теории позволяет объяснить прямолинейное распространение света. Определим амплитуду световой волны в произвольной точке Р, используя метод зон Френеля. Рассмотрим сначала случай падающей плоской волны (рис. 3.2).

Пусть плоский фронт волны F, распространяющейся от расположенного в бесконечности источника света, в некоторый момент времени находится на расстоянии ОР - r₀ от точки наблюдения Р.

Рис. 3.2. Применение принципа Гюйгенса — Френеля к плоской волне: зоны Френеля на поверхности плоского волнового фронта F представляют собой концентрические кольца (для наглядности изображение зон Френеля развернуто на 90°, такими они выглядят из точки Р)

Все точки фронта волны, согласно принципу Гюйгенса - Френеля, испускают элементарные сферические волны, которые распространяются по всем направлениям и через некоторое время достигают точки наблюдения Р. Результирующая амплитуда колебаний в этой точке определяется векторной суммой амплитуд всех вторичных волн.

Колебания всех точек волнового фронта F имеют одинаковое направление и происходят в одной фазе. С другой стороны, все точки фронта F находятся от точки Р на различных расстояниях. Для определения результирующей амплитуды всех волн в точке наблюдения Френель предложил метод разбиения волновой поверхности на кольцевые зоны, называемые зонами Френеля.

Взяв точку Р в качестве центра, построим ряд концентрических сфер, радиусы которых начинаются с r₀ и увеличиваются каждый раз на половину длины волны l/2. При пересечении с плоским фронтом волны F эти сферы дадут концентрические окружности. Таким образом, на фронте волны появятся кольцевые зоны (зоны Френеля) с радиусами r₁, r₂, r₃ и т. д.

Определим радиусы зон Френеля, имея ввиду, что 0А=r₁, 0А²=АР²-0Р², то есть

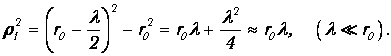
(3.3)

Аналогично находим

(3.4)

Для оценки амплитуд колебаний определим площади зон Френеля. Первая зона (круг):

(3.5)

вторая зона (кольцо):

(3.6)

третья и последующие зоны (кольца):

(3.7)

Таким образом, площади зон Френеля примерно одинаковы, поэтому, согласно принципу Гюйгенса - Френеля, каждая зона Френеля служит источником вторичных сферических волн, амплитуды которых приблизительно одинаковы. Кроме того, колебания, возбуждаемые в точке Р двумя соседними зонами, противоположны по фазе, так как разность хода соответствующих волн от этих зон до точки наблюдения Р равна l/2. Поэтому при наложении эти колебания должны взаимно ослаблять друг друга, то есть амплитуда А результирующего колебания в точке Р может быть представлена в виде знакопеременного ряда

(3.8)

где А₁ - амплитуда колебаний в точке Р возбуждаемых действием центральной (первой) зоны Френеля, А₂ - амплитуда колебаний, возбуждаемых второй зоной, и т. д.

Расстояние от m -й зоны до точки Р медленно растет с номером зоны т. Угол j между нормалью к элементам зоны и направлением в точку Р также растет с т, следовательно, амплитуда А_т колебания, возбуждаемого m -й зоной в точке Р, монотонно убывает с ростом т. Другими словами, амплитуды колебаний, возбуждаемых в точке Р зонами Френеля, образуют монотонно убывающую последовательность:

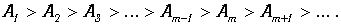
(3.9)

Вследствие монотонного и медленного убывания А_т можно приближенно положить, что амплитуда колебаний от зоны с номером т равна среднему арифметическому амплитуд колебаний от двух соседних зон Френеля:

(3.10)

В выражении для амплитуды результирующего колебания все амплитуды от четных зон входят с одним знаком, а от нечетных - с другим. Запишем это выражение в следующем виде:

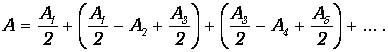
(3.11)

Выражения в скобках на основании (3.10) будут равны нулю, так что

(3.12)

то есть результирующая амплитуда, создаваемая в точке наблюдения Р всей поверхностью волнового фронта, равна половине амплитуды, создаваемой одной лишь центральной (первой) зоной Френеля. Таким образом, колебания, вызываемые в точке Р волновой поверхностью F, имеют такую же амплитуду, как если бы действовала только половина первой (центральной) зоны. Следовательно, свет распространяется как бы в узком канале, сечение которого равно половине первой (центральной) зоны Френеля - мы снова пришли к прямолинейному распространению плоской волны.

Если же на пути волны поставить диафрагму с отверстием, оставляющим открытой только центральную (первую) зону Френеля, амплитуда в точке Р будет равна А₁, то есть в два раза превзойдет амплитуду, создаваемую всем волновым фронтом. Соответственно, интенсивность света в точке Р будет в четыре раза больше, чем при отсутствии преграды между источником света и точкой Р. Удивительно, не так ли? Но чудес в природе не бывает: в других точках экрана интенсивность света будет ослаблена, а средняя освещенность всего экрана при использовании диафрагмы, как и следовало ожидать, уменьшится.

Правомерность такого подхода, заключающегося в делении волнового фронта на зоны Френеля, подтверждена экспериментально. Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны пластинку, которая перекрывает все четные или нечетные зоны Френеля, то можно убедиться, что интенсивность света в точке Р резко возрастет. Такая пластинка, называемая зонной, действует подобно собирающей линзе. Подчеркнем еще раз: зоны Френеля - это мысленно выделенные участки поверхности волнового фронта, положение которых зависит от выбранной точки наблюдения Р. При другой точке наблюдения расположение зон Френеля будет иным. Метод зон Френеля - удобный способ решения задач о дифракции волн на тех или иных препятствиях.

Различают два вида дифракции. Если источник света S и точка наблюдения Р находятся далеко от препятствия, лучи, падающие на препятствие и идущие в точку Р, образуют практически параллельные пучки. В таком случае говорят о дифракции в параллельных лучах, или дифракции Фраунгофера. Если же рассматривается дифракционная картина на конечном расстоянии от препятствия, вызвавшего дифракцию, то говорят о дифракции сферических волн, или дифракции Френеля.

Поиск по сайту: