АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Принцип Ферма

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. ERP-стандарты и Стандарты Качества как инструменты реализации принципа «Непрерывного улучшения»
  3. I. Структурные принципы
  4. II. Принципы процесса
  5. II. Принципы средневековой философии.
  6. II. СВЕТСКИЙ УРОВЕНЬ МЕЖКУЛЬТУРНОЙ КОММУНИКАЦИИ ОТНОСИТЕЛЬНО ПРИНЦИПОВ ПОЛИТИЧЕСКОЙ СПРАВЕДЛИВОСТИ
  7. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  8. II.4. Принципы монархического строя
  9. III. Принцип удовольствия
  10. III. Принципы конечного результата
  11. III. Принципы конечного результата.
  12. IV. Принцип реальности

Итак, волновая оптика способна объяснить явления отражения и преломления света столь же успешно, как и геометрическая оптика. В основу последней, трактующей явления на основе законов распространения лучей, положен принцип Ферма:

Свет распространяется по такому пути, для прохождения которого требуется минимальное время.

Для прохождения участка пути ds свету требуется время

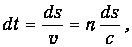
где v=с/п - скорость света в среде. Таким образом, время t, затрачиваемое светом на путь от точки 1 до точки 2, равно

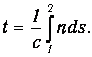
  (1.3)

Введем величину с размерностью длины, которая называется оптической длиной пути:

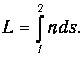
  (1.4)

Пропорциональность t и L позволяет сформулировать принцип Ферма следующим образом:

Свет распространяется по такому пути, оптическая длина которого минимальна.

Рассмотрим путь света из точки S в точку С после отражения от плоскости АВ (рис. 1.9).


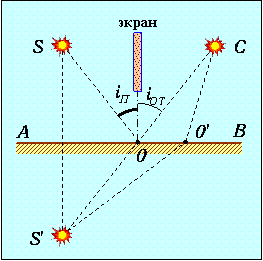
Рис. 1.9. Применение принципа Ферма к отражению света

Непосредственное попадание света из S в С невозможно из-за экрана. Нам надо найти точку О, отразившись в которой луч попадет в точку С. Среда, в которой проходит луч, однородна. Поэтому минимальность оптического пути сводится кминимальности его геометрического пути. Рассмотрим зеркальное изображение S' точки S. Геометрические длины путей SOC и S'OC равны. Поэтому минимальность длины SOC эквивалентна минимальности длины S'OC. А минимальная геометрическая длина пути из S' в С будет соответствовать прямой, соединяющей точки S' и С. Пересечение этой прямой с плоскостью раздела сред дает положение точки О. Отсюда следует равенство углов:

то есть закон отражения света.

Рассмотрим теперь явление преломления света (рис. 1.10).


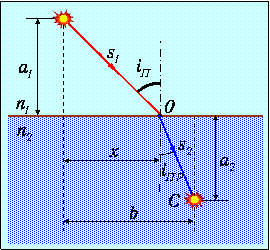
Рис. 1.10. Применение принципа Ферма к преломлению света

Определим положение точки О, в которой должен преломиться луч, распространяясь от S к С, чтобы оптическая длина пути L была минимальна. Выражение для L имеет вид

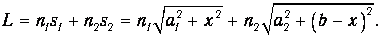
  (1.5)

Найдем величину х, соответствующую экстремуму оптической длины пути:

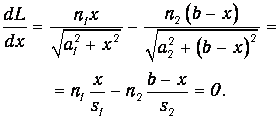
  (1.6)

Отсюда следует

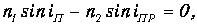
  (1.7)

или

Мы получили закон преломления света.

Принцип Ферма является частным случаем так называемого принципа наименьшего действия, имеющего приложения практически ко всем областям физики. Всякий раз из всех возможных движений системы осуществляется то, для которого некая величина (ее называют действием ) минимальна (точнее, имеет экстремум). В этом проявляется некая «экономность» природы, выбирающей оптимальные пути для перехода системы из одного состояния в другое.


 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)