Полосы равной толщины. Кольца Ньютона

Рассмотрим отражение света от соприкасающихся друг с другом плоско-параллельной толстой стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 2.9). Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный клин (зазор) между пластинкой и линзой. (Вследствие большой толщины пластинки и линзы отраженные от других поверхностей волны интерференционных картин не создают.)

Рис. 2.9. Наблюдение колец Ньютона

При нормальном падении света интерференционная картина имеет вид концентрических окружностей (кольца Ньютона). Каждая из таких интерференционных полос возникает в результате отражения от участков воздушного клина с одинаковой толщиной (вследствие чего их называют интерференционными полосами равной толщины). Определим радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. В этом случае sin i_П=0 и оптическая разность хода равна (в воздушном зазоре п=1):

(2.30)

Из треугольника DCAB имеем (R>>d):

(2.31)

или

(2.32)

Таким образом, для светлых колец (максимумы) разность хода будет

(2.33)

Отсюда следует выражение для радиусов светлых колец:

(2.34)

Радиусы темных колец Ньютона получаются равными

(2.35)

В точке касания пластинки и линзы, то есть при т=0, rт=0, наблюдается минимум интенсивности, обусловленный изменением фазы колебаний на p при отражении световой волны от пластинки.

Пример. В отраженном свете с длиной волны l=546 нм были измерены радиусы двух светлых колец Ньютона, оказавшиеся равными 0.161 см и 0.284 см. Было подсчитано, что между этими кольцами расположено 19 других светлых колец. Определим радиус кривизны линзы.

Пусть меньшее измеренное кольцо Ньютона имеет порядок т, тогда порядок большего равен т+20. Используем (2.34):

Возводя эти равенства в квадрат и разделив одно на другое, получим

Отсюда находим порядок т меньшего из упомянутых колец Ньютона:

и искомый радиус кривизны линзы будет равен

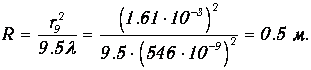
Поиск по сайту: