Структура методов решения задач безусловной минимизации

Последовательность обладает свойством:

(2)

Большинство методов безусловной минимизации предусматривает построение последовательности 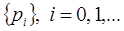направлений движения к минимуму .

Основное отличие одного метода от другого заключается в способе построения . При этом соседние точки последовательности связаны соотношением (см. рис. 2)

(3)

где – параметр, определяющий длину шага вдоль направления , избираемую некоторым определенным способом.

Вектор «сдвига» в направлении равен

. (4)

Таким образом, выполнение одной (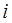 -ой) итерации (или шага) в конкретном алгоритме спуска заключается в определении направления спуска и точки на данном направлении.

Рис. 2. Графическое изображение итерационного шага

Структуру рассматриваемых далее методов безусловной минимизации можно представить следующей схемой (см. рис. 3).

Рис. 3. Структурная схема методов безусловной минимизации

Шаг 0. Выбирается некоторая начальная точка и положительно определенная ()-матрица . Выполняется расчет градиента минимизируемой функции в точке .

Шаг 1. Даны: точка , вектор градиента , ()-матрица 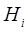. Определяется направление

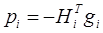. (5)

В общем случае вектор направления является некоторой явной функцией точки , предыдущих точек , ,…, векторов градиентов , ,… минимизируемой функции и матриц , ,… ее вторых производных (матриц Гессе), вычисленных в точках , ,…, т.е.

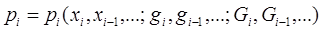. (6)

В выражении (6) зависимость от некоторых групп переменных, например, , ,…, может отсутствовать.

Если существует явная зависимость от предыдущих точек , ,…, или величин, вычисленных в этих точках, то подобный поисковый метод называется методом с памятью. Если же вектор направления явно зависит лишь от величин, вычисленных в точках , то соответствующий метод называется методом без памяти.

В зависимости от максимального порядка производных, входящих в выражение (6), алгоритмы минимизации относятся соответственно к методам нулевого, первого и второго порядков.

Вектор , обычно определяет направление «спуска», т.е. убывания функции . Это означает, что производная функции по направлению отрицательна

(7)

Достаточным условием выполнения этого условия является положительная определенность матриц .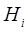

Шаг 2. Рассматривается функция одной переменной

(8)

и выбирается величина , определяющая шаг по направлению и удовлетворяющая условию:

(9)

и некоторым другим требованиям. Например, если дополнительное условие для имеет вид

(10)

то говорят о точном нахождении минимума функции в направлении . Соответствующее будем обозначать , а точку назовем оптимальной в направлении . В некоторых случаях полагают = const, если удовлетворяется условие (9).

Шаг 3. Рассчитываются точка и (в градиентных методах) вектор , а затем формируется матрица .

В зависимости от результата проверки условия остановки работа алгоритма либо прекращается (в этом случае с требуемой точностью является оптимальной точкой), либо осуществляется переход к шагу 1 (). Условием окончания работы алгоритма обычно является неравенство , где – заданное число, или . Используются также и другие условия окончания, например, вместе с , и т.д.

Поиск по сайту: