 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Метод наискорейшего спуска, метод градиента
В классическом методе наискорейшего спуска (методе Коши). в выражении (5) (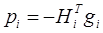
) матрица 
принимается равной 
, 
, где 
– единичная (
)-матрица. Направлением движения здесь является наискорейшее убывание функции в данной точке:
(11)
Точки 
перехода на следующее направление определяются с помощью условия (10) 
, т. е. 
.
Отличием метода градиента от метода наискорейшего спуска заключается в том, что переход на следующее направление определяется с помощью условия (9) 
).
На рисунке направление движения из точки касается линии уровня в точке 
. Траектория спуска зигзагообразная, причем соседние звенья зигзага ортогональны друг другу.
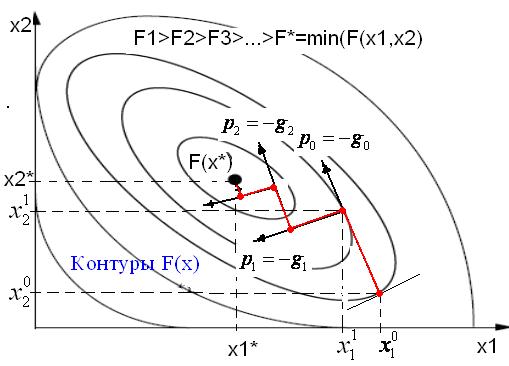
В методе наискорейшего спуска каждое новое направление ортогонально предыдущему, т.к. движение в одном направлении идет до тех пор, пока направление движения не окажется касательным к какой-либо линии постоянного уровня.
Отметим, что в методах наискорейшего спуска и градиента производные 
критерия оптимизации по варьируемым переменным определяются либо аналитически, либо с помощью разностей:
. (12)
В этой формуле нижний индекс обозначает номер компоненты вектора 
.
Использование уравнения (12) связано с тем, что, как правило, при оптимизации реальных систем (технических, химико-технологических и др.) вид математической модели и соответственно целевой функции в явном виде не задан. Имеется только алгоритм, который позволяет при заданных значениях поисковых переменных вычислить значение целевой функции.
Достоинство градиентных методов – простота реализации.
Недостатки:
1) метод является линейным – даже при минимизации квадратичной функции процесс поиска ее минимума теоретически бесконечен;
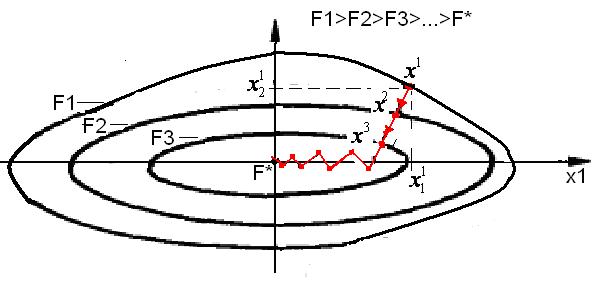
2) для функций с сильно вытянутыми линиями равного уровня (овражные функции) процесс поиска носит явно выраженный зигзагообразный характер и дает слабое продвижение к минимуму; точное определение минимума практически нереально. Направление антиградиента этих функций (см. рис) существенно отклоняется от направления в точку минимума, что приводит к замедлению скорости сходимости.
Поиск по сайту: