АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод сопряженных направлений

Читайте также:
  1. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  2. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  3. I. Методические основы
  4. I. Методические основы оценки эффективности инвестиционных проектов
  5. I. Предмет и метод теоретической экономики
  6. I. Что изучает экономика. Предмет и метод экономики.
  7. II. Метод упреждающего вписывания
  8. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  9. II. Методы непрямого остеосинтеза.
  10. II. Проблема источника и метода познания.
  11. II. Рыночные методы.
  12. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ

Определение: два 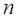-мерных вектора и называют сопряженными по отношению к матрице (или -сопряженными), если скалярное произведение , при .Здесь – симметрическая положительно определенная матрица размером .

Использование векторов, сопряженных относительно некоторой положительно определенной матрицы, составляет основу метода первого порядка, известного как метод сопряженных направлений.

 

Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции. Это существенно увеличивает скорость сходимости и позволяет, например, минимизировать квадратичную функцию с симметрической положительно определенной матрицей за конечное число шагов 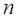, равное числу переменных функции.

Метод Флетчера-Ривса решает эту проблему путем преобразования на каждом шаге антиградиента в направление , -сопряженное с ранее найденными направлениями .

На первом направлении принимается:

(13)

Далее на каждом направлении ищется оптимальная точка:

(14)

 

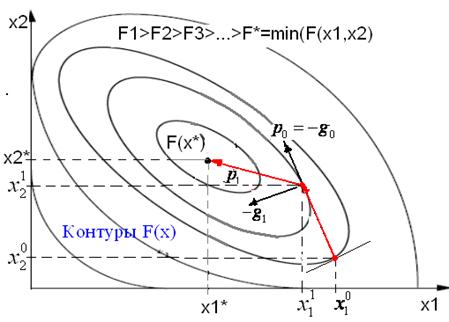
Геометрический смысл траектории спуска в методе сопряженных градиентов показан на рисунке. Из заданной начальной точки осуществляется спуск в направлении . В точке определяется вектор-градиент . Поскольку является точкой минимума функции в направлении , то ортогонален вектору . Затем отыскивается вектор , -сопряженный к . Далее отыскивается минимум функции вдоль направления и т. д.

Методы сопряженных направлений являются одними из наиболее эффективных для решения задач минимизации.

Однако они чувствительны к ошибкам, возникающим в процессе счета. При большом числе переменных погрешность может настолько возрасти, что процесс придется повторять даже для квадратичной функции, т. е. процесс для нее не всегда укладывается в 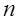шагов.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)