АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Методы первого порядка

Читайте также:
  1. II ОБЩИЕ НАЧАЛА ПУБЛИЧНО-ПРАВОВОГО ПОРЯДКА
  2. II. Методы непрямого остеосинтеза.
  3. II. Рыночные методы.
  4. II. САКРАЛЬНАЯ ГЕОМЕТРИЯ: МЕТАФОРА УНИВЕРСАЛЬНОГО ПОРЯДКА
  5. III. Параметрические методы.
  6. IV. Современные методы синтеза неорганических материалов с заданной структурой
  7. IV.1. Общие начала частной правозащиты и судебного порядка
  8. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  9. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  10. V2: ДЕ 6 - Линейные отображения. Определители второго порядка
  11. А. Механические методы
  12. Автоматизированные методы анализа устной речи

В методах первого порядка (градиентные методы) направление спуска совпадает с направлением антиградиента.

Напомним, что градиентом дифференцируемой функции в точке называется 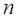-мерный вектор 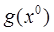, компоненты которого являются частными производными функции, вычисленными в этой точке.

Этот вектор перпендикулярен к плоскости, проведенной через точку , и касательной к поверхности уровня функции , проходящей через точку .

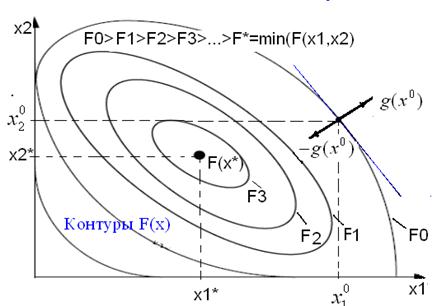
Вектор-градиент направлен в сторону наискорейшего возрастания функции в данной точке. Вектор, противоположный градиенту 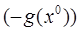, называется антиградиентом и направлен в сторону наискорейшего убывания функции. В точке минимума градиент функции равен нулю.

Градиентные методы отличаются друг от друга способами выбора величины шага.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)