АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Постановка задачи оптимизации. · Постановка задачи оптимизации

Читайте также:
  1. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  2. I. ЗАДАЧИ ПЕДАГОГИЧЕСКОЙ ПРАКТИКИ
  3. I. Ситуационные задачи и тестовые задания.
  4. II. Основные задачи и функции
  5. II. ЦЕЛИ, ЗАДАЧИ И ПРИНЦИПЫ ДЕЯТЕЛЬНОСТИ ВОИ
  6. II. Цель и задачи государственной политики в области развития инновационной системы
  7. III. Цели и задачи социально-экономического развития Республики Карелия на среднесрочную перспективу (2012-2017 годы)
  8. VI. ДАЛЬНЕЙШИЕ ЗАДАЧИ И ПУТИ ИССЛЕДОВАНИЯ
  9. А. Постановка транспортной задачи.
  10. Аналитические возможности, задачи и основные направления анализа СНС
  11. Б. Математическая модель транспортной задачи.
  12. БАЛАНС КОММЕРЧЕСКОГО БАНКА, ЦЕЛИ И ЗАДАЧИ ЕГО АНАЛИЗА

План лекции

· Постановка задачи оптимизации

· Классификация методов решения задач минимизации

· Структура методов решения задач безусловной минимизации

· Методы многомерной безусловной оптимизации

· Методы нулевого порядка.

· Метод покоординатного спуска

· Методы первого порядка

· Метод наискорейшего спуска, метод градиента

· Метод сопряженных направлений

· Методы многомерной оптимизации. Методы второго порядка

· Метод Ньютона

· Квазиньютоновские методы

· Общее правило выбора метода оптимизации

Постановка задачи оптимизации

 

Напомним общую постановку задачи оптимизации

 

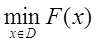, (1)

– критерий оптимальности (целевая функция);

– вектор варьируемых параметров;

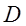– допустимая область значений :

Если 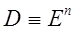– семейство задач безусловной оптимизации.

Если 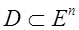– семейство задач условной оптимизации.

 

На прошлой лекции мы показали, что, используя функцию Лагранжа, задача условной оптимизации может быть сведена к задаче безусловной оптимизации.

Рассмотрим методы решения задач безусловной оптимизации.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)