 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Квазиньютоновские методы
Основной идеей квазиньютоновских методов является объединение этапов сбора информации и поиска ее минимума. В этих методах, на основе информации о значениях функции и ее производных в точках поиска, строится некоторая аппроксимация либо самого гессиана 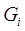 либо обратного гессиана
либо обратного гессиана 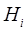 (
(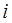 – номер точки).
– номер точки).
Формулы аппроксимирующие либо сам гессиан, либо обратный были выведены из условий:
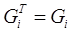
| 
|
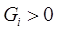
| 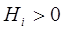 (16) (16)
|
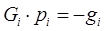
| 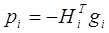
|
В дальнейшем будем рассматривать матрицу аппроксимирующую обратный гессиан 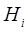 .
.
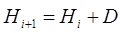 (17)
(17)
Где 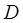 – матрица, найденная по какому либо алгоритму. При выводе аппроксимирующей формулы предполагалось, что матрица
– матрица, найденная по какому либо алгоритму. При выводе аппроксимирующей формулы предполагалось, что матрица 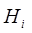 полученная на
полученная на 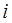 -ой итерации обладает некоторыми положительными свойствами, к примеру, хорошо аппроксимирует обратный Гессиан
-ой итерации обладает некоторыми положительными свойствами, к примеру, хорошо аппроксимирует обратный Гессиан 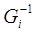 . Поэтому искомая матрица
. Поэтому искомая матрица 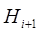 должна минимально отличаться от матрицы
должна минимально отличаться от матрицы 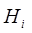 . Таким образом, выражение для матрицы
. Таким образом, выражение для матрицы 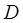 было найдено из условия наименьшего изменения матрицы
было найдено из условия наименьшего изменения матрицы 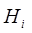 . При этом было выполнено требование, чтобы приближение
. При этом было выполнено требование, чтобы приближение 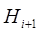 к матрице
к матрице 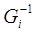 , удовлетворяло условию:
, удовлетворяло условию:
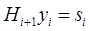 (18)
(18)
где 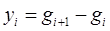 ,
, 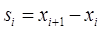 .
.
Методы, удовлетворяющие условию (16), называются квазиньютоновскими методами 1-го рода.
Наибольшее распространение получили формулы:
Давидона-Флетчера-Пауэлла (DFP)
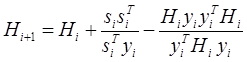 (19)
(19)
Бройдена-Флетчера-Гольдфарба-Шенно (BFGS)
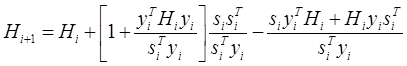 (20)
(20)
В методах второго порядка, как и в методах первого порядка, градиент целевой функции вычисляется аналитически, либо с использованием разностей (12).
Поиск по сайту: