Энтропия источника сообщения

Алфавит (А) – конеч-я сов-сть символов (знаков), с пом. кот. м. предст-ть любое сообщ-е в инф-й системе (ИС). . – i-й символ А.

Мощ-сть А – кол-во символов, сост-щих А (N(A)). Рус-я язык N=33.

Св-ва симоволов А выраж-ся ч/з вероятностные х-ки каждого символа. Вер-сть того, что произв-й символ произв-го док-нта будет буквой : . (1).

Инф-ной х-кой А (ист-ка сообщений на основе этого А) явл-ся энтропия. Ввел понятие Клод Шеннон. Инф-ная энтропия – мера хаотичности инф-ции, неопр-сть появл-я какого-л. символа А. При отсутствии инф-ных потерь численно равна кол-ву инф-ции (бит), которое прих-ся в среднем на 1 символ перед-го сообщ-я.

(2), где , – i-й символ А, – вер-сть 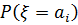. Ед. измер-я – бит.

Энтропия двоичного канала/ист-ка сообщ-й: А сост-т из 2-х символов: , N=2. . . На основ-и (2):

(3) .

Тогда (4)

Если то , т.е. сообщ-е не несет никакой инф-и.

Шеннон предпол-л, что прирост инф-и равен утраченной неопр-сти, и задал требов-я к её измер-ю: 1) мера д.б. непрер-й; т.е. измен-е знач-я ве-ны вер-сти на малую в-ну должно выз-ть малое рез-щее измен-е ф-ции; 2) в случае, когда все вар-нты равновероятны, ув-ние кол-ва вар-нтов (букв) должно всегда ув-ть знач-е ф-ции; 3) д.б. возм-сть сделать выбор в 2 шага, в кот-х знач-е ф-ции конечного рез-та должно явл-ся суммой ф-ций промеж-х рез-тов. Поэтому ф-ция энтропии H д. удовл-ть усл-м: 1) опр-на и непрерывна для всех , где 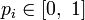для всех и 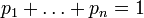. (эта функция зависит только от распределения вероятностей, но не от алфавита.)

2) Для целых положительных n, должно выполняться следующее неравенство:

3) Для целых положительных b_i, где , должно вып-ся рав-во:

Шеннон показал, что единств-я ф-ция, удовл-щая этим требованиям, имеет вид:

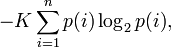где K – константа (нужна для выбора единиц измер-я).

Шеннон опр-л, что измер-е энтропии (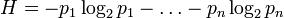), прим-мое к ист-ку инф-и, м. опр-ть треб-я к миним-й пропускной спос-сти канала, требуемой для надёжной передачи инф-и в виде закодир-х двоичных чисел. Для вывода формулы Шеннона необх-мо вычислить мат-е ожид-е «кол-ва инф-и», содерж-ся в цифре из ист-ка инф-и. Мера энтропии Шеннона выражает неувер-сть реализ-и случ-й переменной. Т.о., энтропия явл-ся разницей м/ду инф-й, сод-ся в сообщ-и, и той частью инф-и, кот-я точно известна (или хорошо предсказуема) в сообщении. Примером этого явл-ся избыточ-сть языка – им-ся явные статистич-е закономер-сти в появл-и букв, пар пос-ных букв, троек и т. д.

Энтропия Хартли. Частный случай энтропии Шеннона. Вер-сть появл-я каждого символа А одинакова. Если задано N, то

Хартли предложил хар-ть неопред-сть логарифмом числа n. Т.е. log n явл-ся колич-й мерой неопр-сти. Пусть имеется N сост-й системы S или N опытов с разл-ми, равновозм-ми пос-ми сост-ми системы. Если каждое сост-е системы закодир-ть, напр., двоичными кодами опр-ной длины d, то эту длину необх-мо выбрать так, чтобы число всех разл-х комбинаций было бы не меньше, чем N. Наименьшее число, при кот-м это возможно или мера разнообразия мн-ва сост-й системы зад-ся формулой Р. Хартли: H=k log _а N, где k – коэф-нт пропорц-сти (масштабир-я, в зав-сти от выбранной единицы измерения меры), а - основание системы меры.

Если измерение ведётся в экспоненц-й системе, то k=1, H=lnN (нат); если измерение - в двоичной системе, то k=1/ln2, H=log₂N (бит); если измерение - в десятичной системе, то k=1/ln10, H=lgN (дит).

Пример. Чтобы узнать полож-е точки в системе из 2х клеток т.е. получить некот-ю инф-ю, необх-мо задать 1 вопрос ("Левая или правая клетка?"). Узнав полож-е точки, мы ув-м суммарную инф-ю о системе на 1 бит (I=log₂ 2). Для системы из 4х клеток необх-мо задать 2 аналог-х вопроса, а инф-я равна 2 битам (I=log₂4). Если сист имеет n разл-х сост-й, то макс-е кол-во инф-и равно I=log₂ n.

По Хартли, для того, чтобы мера инф-ции имела практ-ю цен-сть - она д.б. такова, чтобы отражала кол-во информации пропорционально числу выборов.

Пример. Имеются 192 монеты из кот-х одна фальшивая. Опр-м ск-ко взвеш-й нужно произвести, чтобы опр-ть ее. Если положить на весы равное кол-во монет, то получим 2 возм-сти: а) левая чашка ниже; б) правая чашка ниже. Т.о., каждое взвеш-е дает кол-во инф-и I=log₂2=1 и, следов-но, для опр-я фальш-й монеты нужно сделать не менее k взвеш-й, где k удовл-т условию log₂2k³ log₂192. Отсюда, k=7. След-но, нам необходимо сделать не менее 7 взвешиваний (достаточно семи).

Формула Хартли отвлечена от качеств-х, индивид-х св-в рассм-мой системы (кач-ва инф-ции, сод-щейся в системе, в проявлениях системы с помощью рассматриваемых N состояний системы). Это основная положит-я сторона этой формулы. Но имеется и основная отриц-я сторона: формула не учит-т различимость и различность рассматриваемых N состояний системы.

Поиск по сайту: