Особенности симметричных и ассиметрич. систем шифрования данных

По назначению используемого ключа современ. криптогр. системы дел. на:

1) симметричн. В прям. и обратн. преобраз. (зашифр./ расшифр.) используется одинаковый ключ. Ключ является тайным. Алгоритм известен.

Например пусть используется симметричный блочный алгоритм, длина блока 4 символа. Алгоритм преобразования основывается на вычислении по mod 2, расшифрование тоже.

М = 10101100 К = 0101 (тайная информация) Т.к. длина блока 4, то К тоже 4.

Зашифрование:

Сообщение М делим на блоки в соотв. С принятой длиной m1 = 1010, m2 = 1100.

C = f (алгоритм, К, М) – шифртекст (шифрограмма), справедливо для любой криптограф. системы.

При использовании блочного алгоритма шифрования текста С = с₁…с _l

В нашем случае С= с1с2

с1 = m1 + К = 1010+0101=1111 (!!! Здесь и до конца шпоры + это сложение по mod 2).

с2 = m2 + К = 1100+0101=1001

С = 11111001 такой шифртекст по открытым каналам поступает к получателю.

Обратное преобразование (расшифрование):

M’ = f (C, K, алгоритм)

M’ = m1’m2’

m1’ = c1 + K = 1111+0101=1010= m1

m2’ = c2 + K = 1001+0101=1100= m2

M’ = 10101100 = M

В реальн. системах помимо вычислит. операций исп-ся множествен. подстановки и перестановки. Наи> известн. и 1 из стандартизован. — стандарт. DES, принят в США и позднее исп-ся во всем мире. Длина ключа = 64 bit из кот. 54 вычислительных, 8 — биты чётности (CRC). Особ-ти этой системы: 1) хранение/ обмен ключами; 2) «+» сравнит-но не > длина ключа; вычисл. производ-ся быстрее, т.к. не > длина ключа; 3) «-» при < длине ключа проще его найти хотя бы методом простого перебора.

2) асимметр. Системы предполагают, что при прям. и обратн. преобраз. исп-ся различн. ключи, взаимосвязан. м-у собой по известн. законам. Известный метод RSA.

Криптографическая система шифрования данных RSA (1978 г.) является одной из первых практически реализованных идей Диффи и Хеллмана. RSA предполагает, что каждый пользователь независимо от других пользователей генерирует свои собственные ключи (тайный и публичный): тайный известен только пользователям, публичный – общедоступен.

В RSA n представляет собой составное число , числа p и q – большие целые простые (примерно одного порядка), n – открытое число, p и q – тайные.

Задача злоумышленника – разложить n (известное) на простые сомножители.

Система предполаг., что кажд. пользователь может независ. создать свой ключ.

Математической основой системы является теорема:

Для целых чисел e и d, удовлетворяющих соотношению e*d mod =1, где

1) (ф-ция Эйлера) и M (сообщение) должны быть взаимно простыми;

2) должны быть взаимно простыми пары чисел e и n, d и n;

выполняется равенство (M^e mod n) ^d mod n = M.

Процедура генерации (создания) ключа:

1. Выбрать сопоставимые по величине 2 простых числа p и q.

2. Вычислить (n является открытым числом).

3. Вычислить функцию Эйлера [определяет количество целых положительных чисел, меньших n и взаимно простых с n; n>1; если n – простое число, то 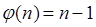; если , где p и q – простые числа, то ]:

( является закрытым числом).

4. Случайным образом выбирается число e (или d), которое должно быть взаимно простым с .

5. Вычисляется мультипликативное инверсное значение к величине, определенной в п. 4 в соответствии со следующими формулами:

Если в п. 4 выбрано e, то в п. 5 используют соотношение: .

Принято считать, что пара (e,n) – открытый ключ пользователя, а число d – закрытый ключ (d,n).

Пример1: 1. Пусть p = 3, q = 7.

2. Тогда .

3. Вычисляем .

4. Выбираем e = 17 (взаимно простое с 12).

5. Решаем уравнение или .

Открытый ключ: (17,21); закрытый: (5) или (5,21).

А отправляет сообщение В. Используются ключи получателя В и при зашифровании и при расшифровании. e и n – общедоступны и находятся на специализированных сайтах.

Действия А: 1. Создание шифр-текста: .

Если М поделено на блоки одинаковой длины (m¹, m², …, m^L), то С = с¹, с², …, с^L, где .

2. Отправка на адрес В шифр-текста С.

Действия В: 1. Получение: С = с¹, с², …, с^L.

2. Расшифрование: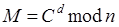

В использует соответствующий тайный ключ d.

Если сообщение разделено на блоки: .

Пример2: Открытый ключ: (17,21); закрытый: (5,21). Предполагается, что сообщение М состоит из 5 символов.

Сообщение М делится на блоки одинаковой длины по одному символу.

Пусть М = 12345 и m¹ = 01, m² = 02, …, m⁵ = 05.

Процедура зашифрования:

, , ,

, .

Шифр-текст: С = 01 11 12 16 17.

Процедура расшифрования:

, , ,

, . Имеем: М = 12345.

Поиск по сайту: