Постановка задачи оптимизации

Задача оптимизации задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором лин. и/или нелин. равенств и/или неравенств.

Суть методов оптимизации (оптимального программирования) заключается в том, чтобы, исходя из наличия определенных ресурсов, выбрать такой способ их использования (распределения), при котором будет обеспечен максимум или минимум интересующего показателя

Оптимизация – это целенаправленная деятельность, которая заключается в получении наилучших результатов при соответствующих условиях.

Постановка задачи оптимизации:

Включает 2 объекта:

1. целевая ф-ция f(x) где х (x1, x2, …, xn)

2. определяется область допустимых значений D x D

Требуется f(x) à min (max) x D

Классификация задач оптимизации:

1. без ограничений f(x,y) = (x - 1)² + (y - 3)² + 1

2. с ограничениями

напр f(x,y)= x² + y²

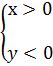
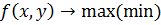
Если целевая ф-ция f(x) и ф-ция описывающая ограничения на аргументы целевой ф-ции, являются линейными ф-циями своих аргументов, то задача оптимизации называется задачей линейного программирования.

Если целевая ф-ция или хотя бы 1 из уравнений, описывающих ограничения, является нелинейной ф-цией своих аргументов, то задача оптимизации называется задачей нелинейного программирования.

Итак, для решения задачи оптимизации необходимо:

а) составить математическую модель объекта оптимизации,

б) выбрать критерий оптимальности и составить целевую функцию,

в) установить возможные ограничения, которые должны накладываться на переменные,

г) выбрать метод оптимизации, который позволит найти экстремальные значения искомых величин.

Поиск по сайту: