Особенности двоичных систем передачи информации

Дост-ва двоичной системы счисления: простота реализ-и проц-в хран-я, пере-дачи и обработки инф-и на ПК, для ее реализ-и нужны эл-нты с 2мя возможными сост-ми, а не с десятью, предст-е инф-и посредством только 2х сост-й надежно и помехоуст-во, возм-сть прим-я алгебры логики для вып-ния логич-х преобр-й.

Недостатки двоичной системы счисления: код числа п/с послед-сть из 0 и 1. Большие числа занимают дост-но бол-е число разрядов. Быстрый рост числа разрядов – самый существенный недостаток двоичной системы счисления.

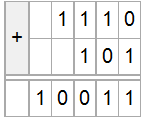Таблица сложения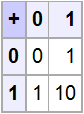

Пример сложения «столбиком» (14 + 5 = 19):

Таблица умножения

Пример умножения «столбиком» (14 × 5 = 70):

Для преобр-я из двоичной системы в десятичную исп-т следующую таблицу степеней основания 2:

512 256 128 64 32 16 8 4 2 1

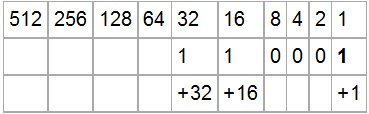
Преобр-е двоичных чисел в десятичные: дано двоичное число 110001. Для перевода в десятичное запишите его справа налево как сумму по разрядам:

Преобр-е десятичных чисел в двоичные: нужно перевести число 19 в двоичное:

19 /2 = 9 с остатком 1

9 /2 = 4 c остатком 1

4 /2 = 2 с остатком 0

2 /2 = 1 с остатком 0

1 /2 = 0 с остатком 1

Длим каждое частное на 2 и запис-м остаток в конец двоичной записи. Прод-м деление до тех пор, пока в делимом не будет 0. В рез-те получаем число 19 в двоичной записи: 10011.

Преобр-е дробных двоичных чисел в десятичные: нужно перевести число 1011010.101 в десятичную систему:

Преобр-е дробных десятичных чисел в двоичные: * Вначале переводится целая часть десятичной дроби в двоичную систему счисления; * Затем дробная часть десятичной дроби умнож-ся на основ-е двоичной системы счисления; * В получ-м произвед-и выд-ся целая часть, кот-я приним-ся в кач-ве знач-я 1-го после запятой разряда числа в двоичной системе счисления; * Алгоритм заверш-ся, если дробная часть получ-го произвед-я = 0 или если достигнута требуемая точ-сть вычисл-й. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число. Перевод целой части дает 206₁₀=11001110₂ по ранее опис-м алг-мам; дроб-ю часть умнож-м на основ-е 2, занося целые части произв-я в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0.232.232 • 2 = 0.464.464 • 2 = 0.928

.928 • 2 = 1.856.856 • 2 = 1.712.712 • 2 = 1.424

.424 • 2 = 0.848.848 • 2 = 1.696.696 • 2 = 1.392

.392 • 2 = 0.784 и т.д.

Получим: 206,11610=11001110,0001110110₂

Двоичная система исп-ся в цифр-х ус-вах, поскольку является наиболее простой и соотв-т требованиям: Чем меньше значений сущ-т в системе, тем проще изготовить отд-е элементы, оперирующие этими знач-ми. В частности, две цифры двоичной системы счисления м.б. легко предст-ны многими физ-ми явл-ми: есть ток (ток больше пороговой в-ны) – нет тока (ток меньше пороговой в-ны), индукция магн-го поля больше пороговой в-ны или нет (индукция магнитного поля меньше пороговой величины) и т. д.

Чем меньше кол-во сост-й у элемента, тем выше помехоуст-сть и тем быстрее он может работать. Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.

Поиск по сайту: