 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
КЛАССИФИКАЦИЯ СИГНАЛОВ
Сигнал — материальный носитель информации, представляющий собой некий физический процесс, один из параметров которого непосредственно связан с измеряемой физической величиной. Этот параметр называется информативным.
Измерительный сигнал — сигнал, который обязательно дает количественную оценку измеряемой физической величине.
ГОСТ 16465 - 70
«Сигналы технической радиоэлектронной теории» Классификация измерительных сигналов (ИС):
1. По характеру измерения во времени, может быть:
■ Постоянный сигнал — сигнал, который не изменяется во времени.

■ Переменный сигнал. В свою очередь который подразделяется на непрерывный

и импульсный (колебания, действующие определенный конечный отрезок времени). Примером может служить радио и импульсы.

Жирным выделена видимая часть Ue(t). Up(t)=Ue(t)cos((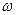 ot+
ot+  ).
).
2. По характеру измерения информационного и временного параметра подразделяются на:
■ Аналоговый - сигнал, описывающийся непрерывной или кусочно-непрерывной функцией.
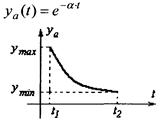
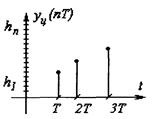
■ Дискретный сигнал — сигнал, изменяющийся дискретно по времени.
Описывается решетчатыми функциями.
T- интервал дискретизации; n - целое число.
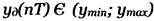 - интервал выборки.
- интервал выборки.

Достоинства: нет необходимости поддерживать в течении какого - то времени, что дает возможность в организации многоканальной связи по одной линии (мультиплексирование каналов)
■ Квантовые сигналы — сигналы, квантованные по уровню.
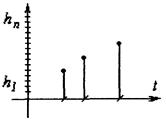
h  =n*q, где q - квант; п - число квантов.
=n*q, где q - квант; п - число квантов.
■ Цифровой сигнал - сигнал квантования по уровню и дискретизированный по времени.
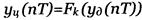 - функция квантования.
- функция квантования.


Для цифровых сигналов удобна система представления фиксированных значений в виде чисел. (Например: двоичная система исчисления). Для восьмиуровневого квантования необходим трёхразрядный двоичный код).
Число уровней квантования N и наименьшее число разрядов m двоичных чисел:
m=int(log2N), где int(A) - наименьшее целое число наименьшего число А.
С уменьшением кванта  h увеличивается разрядность, уменьшается быстродействия передачи сигнала.
h увеличивается разрядность, уменьшается быстродействия передачи сигнала.
3. По степени наличия априорной информации о характере изменения ИС:
■ Детерминированные сигналы - определенные. Сигналы, мгновенное значение которых можно предсказать в любой момент времени.
■ Квадетерминированные - с частично известными параметрами.
■ Случайный - сигнал, поведение которого предсказать невозможно.
Виды детерминированных сигналов:
Элементарные - тестовые сигналы. Предназначены для анализа и проверки радиотехнических устройств (к ним относятся элементарные и ряд сложных).
· Постоянные:

Временные представления элементарных функций:
•Единичная функция. Функция Хевисайда
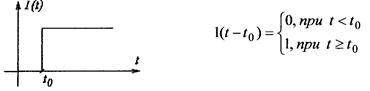
 •Дискретное представление
•Дискретное представление
•Дельта - функция (импульс)

•Дискётная S – функция:
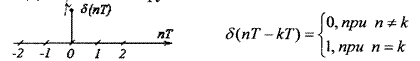
Связь между единичной и δ - функцией:
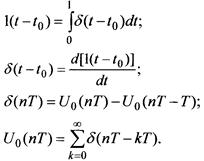
Стробируя непрерывный сигнал, мы получаем дискретный. Процесс стробирования записывается:

Согласно уравнению: если непрерывную функцию умножить на  и проинтегрировать по времени, то результат будет равен мгновенному значению непрерывной функции в точке t
и проинтегрировать по времени, то результат будет равен мгновенному значению непрерывной функции в точке t  , где сосредоточен импульс.
, где сосредоточен импульс.
Структурная модель выглядит следующим образом:
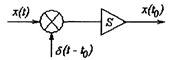
Идеальный дискретный сигнал:

где у(k 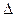 Т) - значение непрерывного сигнала в k- омшаге дискретизации.
Т) - значение непрерывного сигнала в k- омшаге дискретизации.
• Гармонический сигнал.
Моногармоническими сигналами считаются сигналы, изменяющиеся во времени, согласно функциям sin и cos. Все остальные сигналы - полигармонические, так как состоят из множества гармонических составляющих с разными частотами.
y(t)=ymsin(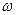 t+
t+  ),
),
где ут - пиковое значение; Т - период времени;  - начальная фаза.
- начальная фаза.
Сложные сигналы:
· Прямоугольный импульс.
y(t)=ym[1-(t-to)-1-(t-to- 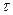 )],
)],
где 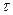 - длительность импульса.
- длительность импульса.

q - скважность импульса (q=T/ 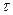 ). Если q=2, то последовательность импульсов называется меандром.
). Если q=2, то последовательность импульсов называется меандром.

 обычно больше, чем
обычно больше, чем 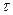 н.
н.
· Измерительные сигналы с линейными участками нарастания - пилообразные сигналы.
а) однополярные
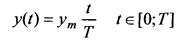


 б) знакопеременные
б) знакопеременные
К сложным измерительным сигналам относится любой модулированный сигнал.
Говоря о детерминированных сигналах, их подразделяют на периодические и непериодические.
Периодические сигналы:
Периодические сигналы - сигналы, значения которых повторяется через определенные интервалы времени. Периодический сигнал может содержать одну гармонику. А может много - полигармонический сигнал. Поэтому для описания периодических сигналов часто используют спектральное (частотное) представление, используя преобразование Фурье.
Периодический сигнал часто характеризуется спектром, используя преобразование Фурье.

где  и
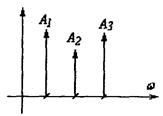
и  - амплитуда и фаза n-ой гармоники соответственно. Множество Аn -амплитудный спектр. Множество
- амплитуда и фаза n-ой гармоники соответственно. Множество Аn -амплитудный спектр. Множество  составляет фазовый спектр. А0 -постоянная составляющая.
составляет фазовый спектр. А0 -постоянная составляющая.
Линейчатый амплитудный спектр выглядит следующим образом:
Интегральные параметры:
· Среднее значение постоянной составляющей:
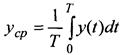
· Средневыпрямленное значение:

· Среднеквадратичное (действительное) значение:
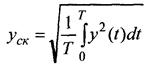
Непериодические сигналы:
Спектральная функция:
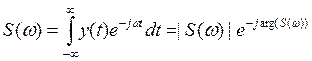
|  | - спектральная плотность.
| - спектральная плотность.
4. По размерности подразделяются:
■ Одномерный сигнал x(t);
■ Многомерный сигнал V(x  (t), x2(t),...).
(t), x2(t),...).
Основные способы описания сигналов:
1)представление в функции времени x(t),
2)представление в операторной форме x(p),
3)представление в виде функции частоты x(w),
4)представление в виде совокупности сигналов.
Принцип динамического представления сигнала – реальный сигнал представляется суммой элементарных сигналов, возникающих в последовательные моменты времени. Если длительность отдельных сигналов ® 0, то в пределе получим точное описание исходного сигнала.
К элементарным относят единичный импульс  , единичную функцию
, единичную функцию  и синусоидальное воздействие.
и синусоидальное воздействие.
1) Импульсной d-функцией называется функция равная нулю по всюду, кроме начала координат, принимающая бесконечное значение в начале координат, причем так что интеграл от нее по любому интервалу, содержащему начало координат равен единице.
единичный импульс (d-функция)  .
.
 , где t- момент действия импульса.
, где t- момент действия импульса.
d-функция- математическая модель короткого внешнего воздействия с единичной площадью. Это идеализированный сигнал, характеризуемый малой длительностью, с ¥ уровнем, площадью, равной единице.
2)  - единичная функция (функция Хэвисайда, функция включения, ступенчатая функция).
- единичная функция (функция Хэвисайда, функция включения, ступенчатая функция).
|
|
|

Динамическое представление сигнала посредством d-функции 
Принцип динамического представления сигнала – реальный сигнал представляется суммой элементарных сигналов, возникающих в последовательные моменты времени. Если длительность отдельных сигналов ® 0, то в пределе получим точное описание исходного сигнала.
Существует два способа динамического представления (ДП)
1)ступенчатой функцией через равные промежутки времени Δ.
2)прямоугольными импульсами

 1
1












 2
2





 D®0
D®0













0 Δ 2Δ 3Δ …
Опишем аналоговый сигнал суммой примыкающих друг к другу прямоугольных импульсов.
 S(t) S(tk) S(t)
S(t) S(tk) S(t)


















 1 2 K
1 2 K







 0 Δt 2Δt tk kΔt t
0 Δt 2Δt tk kΔt t
если SK- значение сигнала на K-ом отсчете, то элементарный импульс с номером K опишется во времени как
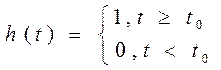 ,
, 
Исходный сигнал должен рассматриваться как сумма элементарных сигналов в соответствии с принципами динамического представления сигналов


в этой å отличен от нуля один член соответствующий  , удовлетворяющий условию
, удовлетворяющий условию 

h(t) – скачкообразная функция, функция Хевисайда (включения)
Переходим к пределу, Dt®0,
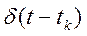
 |

дифференциал
Заменяем å -  по формальной переменной t,
по формальной переменной t, 
 ;
;

Физическая размерность d - функции такая же, как и у частоты; с-1  .
.
Следовательно, если непрерывную функцию  умножить на d - функцию и проинтегрировать по времени, то результат будет равен значению непрерывной функции в точке, где сосредоточен d-импульс. Это фильтрующее свойство d- функции.
умножить на d - функцию и проинтегрировать по времени, то результат будет равен значению непрерывной функции в точке, где сосредоточен d-импульс. Это фильтрующее свойство d- функции.
Поиск по сайту: