Преобразование Карунена-Лоэва

Как уже было отмечено, выбор вида базисных функций в значительной степени определяет погрешность представления при ограниченном количестве спектральных составляющих и сложность алгоритма оптимальной обработки сигнала 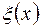. Известно, что для центрированного случайного процесса с непрерывной корреляционной функцией математическое ожидание интегральной среднеквадратической ошибки при представлении процесса 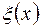рядом (1.2)

(1.12)

при любом фиксированном N будет минимальным, если базисные функции удовлетворяют однородному уравнению Фредгольма второго рода

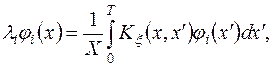(1.13)

где 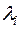- собственные значения ядра

Следовательно, при использовании таких функций в качестве базиса обобщённого ряда Фурье, коэффициенты разложения случайного процесса оказываются некоррелированными, а исходное разложение (1.2) называется преобразование Карунена-Лоэва (ПКЛ). Данное преобразование является оптимальным для представления непрерывных сигналов по отношению к критерию среднеквадратической ошибки. Если в качестве ортонормированного базиса выбрана система собственных функций случайного процесса, то достигается максимальное сжатие информации в том смысле, что энтропия распределения энергии случайного процесса минимальна [29].

С энергетической точки зрения базис Крунена-Лоэва позволяет обеспечить наибольшую концентрацию энергии случайного процесс с минимальной по ширине полосы.

Отмечено [21], что ПКЛ обеспечивает наибольшую из всех известных концентрацию энергии спектра изображения.

Несмотря на перечисленные примечательные свойства, применение непрерывного ПКЛ в значительной степени ограничивается тем обстоятельством, что процедура отыскания решений уравнений (1.13) в общем виде неизвестна (за исключением ряда частных случаев).

При цифровой обработке случайных сигналов используется дискретное ПКЛ. Однако метод Карунена-Лоэва не находит широкого применения при обработке массивов случайных процессов с высокой размерностью. Это обусловлено значительными вычислительными затратами на всех этапах многоступенчатой процедуры оптимизации. По этой причине метод Карунена-Лоэва применяется для сжатия процессов только с невысокой размерностью массивов данных и низкой степенью изменчивости. Поэтому во многих практических задачах используются традиционные разложения в традиционных базисах Фурье, Уолша, Хаара, эффективных в вычислительном отношении. Их иногда называют псевдооптимальными по той причине, что они для ряда случайных процессов уступают методу Карунена0Лоэва по экстремальным свойствам, но превосходят его в вычислительном отношении, поскольку не требуют расчёта значений базисных функций, а также обеспечивают быстрое вычисление коэффициентов разложения.

Поиск по сайту: