Энергия сигнала представленного в форме обобщенного ряда Фурье

Рассмотрим некоторый сигнал S(t), разложенный в ряд по ортонормированной базисной системе 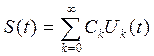и вычислим его энергию, непосредственно подставив этот ряд в соответствующий интеграл:

(*).

Поскольку базисная система функций ортонормированна, в сумме (*) отличными от нуля окажутся только члены с номерами i=j.

Отсюда .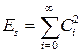

Смысл формулы: энергия сигнала есть сумма энергий всех компонент из которых складывается обобщенный ряд Фурье.

Разложение базиса по ортонормированным базисам:

Запишем энергию суммы двух сигналов:

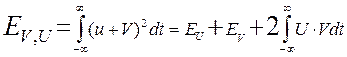
Последнее слагаемое будет представлять собой взаимную энергию.

- взаимная энергия

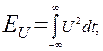
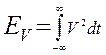
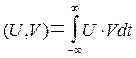- скалярное произведение.

Два сигнала называются ортогональными, если их скалярное произведение равно нулю.

Предположим, что в некотором пространстве сигналов задана система ненулевых функций φ0(x)...φn(x), причем выполняется на конечном отрезке [a,b] условия:

1) Функции должны быть ортогональными, то есть

[a,b] – интервал ортогональности.

2) Функции должны иметь единичную норму:

При выполнении данных условий говорят, что система функций

{ φn(x) } ортонормированна.

Система нормированных функций, каждая из которых попарно ортогональна, называется ортонормированной.

Доказано, если в линейном пространстве сигналов существуют φ1(t), φ2(t)... φn(t) и эта система функций является нормируемой, то любую кусочно-непрерывную функцию f(x) можно разложить в ряд Фурье, если оно удовлетворяет условиям Дирихле:

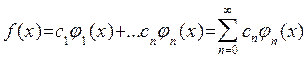- обобщенный ряд Фурье, где

- i-ый коэффициент ряда Фурье, так как необходимо.

На геометрическом языке. Ci – i проекция исследуемого сигнала на ортонормируемый базис.

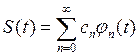
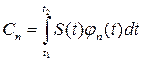
Представление сигнала по ортогональному базису называется обобщенным рядом Фурье. Коэффициентами такого рода служат скалярные произведения разлагаемого сигнала и соответствующих базисных векторов.

Лекция №4

Поиск по сайту: