Разложение сигнала по ортогональным полиномам

Широкое применение находит разложение в ряд Фурье по классическим ортогональным полиномам [28].

Рассмотрим подробнее ортогональную систему функций Лагерра. Полиномы Лагерра являются решением определённого вида линейных дифференциальных уравнений второго порядка и определяются следующим образом:

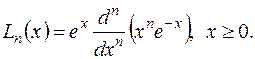(1.4)

Как видно, аппроксимировать ортогональными функциями Лагерра удобно сигналы, аналитические выражения которых описываются произведением полиномов на экспоненциальные функции. Математическая запись полиномов Лагерра первых восьми порядков имеют вид:

(1.5)

Выражение для полиномов более высокого порядка очень громоздки и здесь не приводятся, хотя они получены из общего выражения (1.4) и используются в вычислительных программах.

Функции Лагерра (рис. 1.1) в отличие от полиномов Лагерра являются сходящимися и определяются формулой:

(1.6)

Выражение для ряда Фурье-Лагерра имеет вид:

(1.7)

где - коэффициенты ряда, вычисляемые по общей формуле для обобщённого ряда Фурье (1.3):

(1.8)

Кроме того, наиболее важное теоретическое и практическое значение имеют следующие системы классических ортогональных полиномов:

1) многочлены Чебышева первого рода ортогональные на отрезке [-1;1] с весовой функцией вида

2) многочлены Лежандра ортогональны на отрезке[-1;1];

3) Многочлены Эрмита ортогональны на интервале 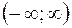с весовой функцией

Особенностью классических полиномов является возможность их рекуррентного вычисления. Они также допускают разложения в ряды Фурье.

Классические полиномы находят широкое применения при решении задач аппроксимации, интерполяции и экстраполяции функций, в особенности для функций с большим числом непрерывных производных.

При выборе полиномов важное значение имеет вид весовой функции, соответствующей тому или иному виду полинома. Этот выбор должен быть тесно увязан с характером аппроксимируемой функции 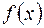: весовая функция должна достигать максимума на участке, где требуется наилучшая аппроксимация. При этом появляется возможность уменьшения числа членов ряда при заданной допустимой ошибке аппроксимации. Выбором весовой функции можно также осуществлять аппроксимацию процессов конечной длительности полиномами, определёнными на бесконечном отрезке. Для этого необходимо, чтобы эффективная длительность весовой функции была близка к длительности аппроксимируемого сигнала.

Поиск по сайту: