Комбинаторные комбинации и числа

Комбинаторика (комбинаторный анализ, комбинаторная математика) – это раздел математики, изучающий способы построения подмножеств некоторого конечного множества с заданными ограничениями.

Сами подмножества при этом называются комбинаторными конфигурациями или выборками.

Предмет комбинаторики составляют следующие задачи:

- подсчет числа комбинаторных конфигураций (комбинаторные числа);

- определение системы условий существования заданных комбинаторных конфигураций;

- разработка алгоритмов построения и генерации комбинаторных конфигураций;

- решение оптимизационных задач.

Эти задачи находят самое широкое применение в теории алгоритмов, теории вероятностей, теории кодирования и т.д.

Так как в комбинаторике используются только конечные множества , содержащие элементов, то принято в первую очередь указывать мощность множества:

-множество .

Опр.2.1.1. Множество 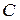, имеющее несколько экземпляров одного и того же элемента называется мультимножеством.

Пример.

– мультимножество. ▲

Опр.2.1.2. Выборкой называется всякое мультимножество, элементы которого выбираются из элементов множества А. Число элементов в выборке определяет ее объем.

Пример.

– 4-выборка. ▲

Замечание: В лекции 1, где рассматривались элементы множеств, мультимножества не вводились, т.е. множества , , не различались и рассматривались как одно и то же множество .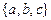

Опр.2.1.3. Выборка, в которой порядок записи элементов не учитывается, называется сочетанием, а в которой учитывается перестановкой.

Введение - сочетаний и -перестановок охватывает все типы выборок. При этом нет необходимости отдельно вводить понятие размещения, т.к. размещение – это -перестановка без повторений.

Рассмотрим основные правила комбинаторики.

I. Правило суммы (закон аддитивности)

Число способов, которыми можно выбрать элементы - множества и элементы -множества при условии, что , равно . С использованием понятия мощности конечных множеств это правило можно записать как

, если . (2.1.1)

Пример.

Лекции по физике посещают 20 студентов, а лекции по теоретической механике – 30, сколько студентов посещают указанные лекции, если они происходят в одно и то же время?

Решение:

Введем следующие множества:

{студенты, посещающие физику}; ;

{студенты, посещающие математику}; .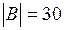

По условию 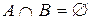. Тогда согласно формуле (1) находим . ▲

II. Правило произведения (закон мультипликативности)

Число способов выбора элементов из декартового произведения двух множеств А и В объемом и равно произведению :

. (2.1.2)

Пример.

Пусть имеется 5 различных конвертов и 6 различных марок. Сколькими способами можно отправить письмо в конверте с маркой?

Решение:

Введем множества: {конверты}; {марки}; {(конверт, марка)}. Таким образом . ▲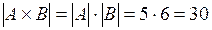

В комбинаторике основными комбинаторными числами являются:

– число различных упорядоченных выборок с повторением из -множества А;

– число различных упорядоченных выборок без повторений из -множества А;

– число различных неупорядоченных выборок (сочетаний) без повторений из А;

– число различных сочетаний с повторениями из -множества А.

Теорема 2.1.1. Если выборка составляется из -множества А, то введенные выше числа вычисляются по формулам:

1). 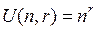, (2.1.3)

2). , (2.1.4)

3). , (2.1.5)

4). . (2.1.6)

Доказательство:

1). Если – множество различных упорядоченных –выборок с повторениями, то . Поэтому .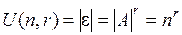

2) Для упорядоченной выборки, не допускающей повторений элементов, первый элемент можно выбрать способами, второй и т.д. Последний элемент выбирается из оставшихся элементов. Поэтому получаем

(или более строго на языке множеств:

).

3) Если имеется -сочетание без повторений, то упорядочить его можно способами. Поэтому

.

4) Для подсчета числа различных -сочетаний с повторениями удобно сопоставить пронумерованным элементам множества А ячейки, которые образованы стенкой. Тогда необходимая выборка реализуется как конфигурация размещения неразличимых шариков в ячеек:

.

Число шариков в конкретной ячейке указывает число экземпляров соответствующего элемента из А в выборке, а число различных выборок будет равно числу перестановок шариков и внутренних стенок. Однако при этом в силу неразличимости шариков и стенок необходимо исключить перестановки между шариками и перестановки между стенками. Таким образом, получим

.

Что и требовалось доказать. ■

Поиск по сайту: