АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Разбиения множеств

Читайте также:
  1. Матричный метод разбиения
  2. Мощности конечных множеств.
  3. Основные тождества алгебры множеств.
  4. Отображения множеств. Взаимно однозначные соответствия.
  5. Процесс разбиения жесткого диска на логические
  6. Прямое произведение множеств.
  7. Способ разбиения по эквивалентности
  8. Сравнение множеств.
  9. Шаг разбиения для равноотстоящих узлов определяем по формуле
  10. Эквивалентность множеств. Мощность множеств.

 

Еще одни важный тип комбинаторных конфигураций составляет разбиение множества на непустые подмножества.

Вначале зафиксируем тип разбиения и решим следующую задачу. Разобьем -множество А на семейство подмножеств так, чтобы в первом подмножестве было элементов, во втором элементов и т.д., т.е. . Очевидно, что должно выполняться равенство

. (2.2.1)

Спрашивается, сколько различных разбиений такого типа существует.

 

Теорема 2.2.1. Число различных разбиений -множества А на подмножеств с фиксированным числом элементов равно

. (2.2.2)

 

Доказательство:

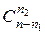Число способов выбора элементов для первого подмножества разбиения равно , для второго – , для третьего – , и т.д. В результате для искомого числа находим

 

■

 

Замечание: Формулу (2.2.2) можно также просто получить, используя модель построения разбиения с помощью системы шариков и стенок.

 

Теперь перейдем к более сложной задаче определения числа различных разбиений элементного множества на классов, когда число элементов в подмножествах не фиксировано. Единственное условие – отсутствие пустых подмножеств.

 

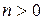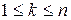Опр. 2.2.1. Пусть , а . Число различных разбиений -множества А на непустых классов называется числом Стирлингавторого рода и обозначается как .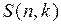

 

Теорема 2.2.2. Число Стирлинга 2го рода 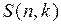обладает следующими свойствами:

1). ; (2.2.3)

2). 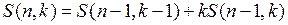, если , . (2.2.4)

 

Доказательство:

1). Понятно, что если 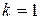, то разбиение содержит одни элемент – само множество А, следовательно . Если же , то опять имеем единственное разбиение, состоящее из одноэлементных подмножеств , поэтому .

2). Если , то все возможности исчерпываются только двумя уже рассмотренными случаями: .

Пусть , а 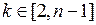(случай рассмотрен в п.1). Удалив из А последний элемент , получим -множество 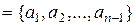. Далее рассмотрим два типа разбиений множества А:

I тип: одноэлементное подмножество составляет отдельный класс разбиения;

II тип: не является отдельным классом разбиения.

Тогда число разбиений множества на классов Iго типа равно числу разбиений множества на класс, т.е. . А число разбиений IIго типа равно числу всех различных разбиений множеств на классов, причем в каждый класс разбиения можно добавить элемент , т.е. имеем

.

В сумме получаем

,

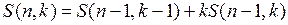что и требовалось доказать. ■

 

Следствие. Число различных разбиений -множества на 2 класса вычисляется по формуле

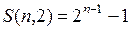для . (2.2.5)

 

Опр.2.2.2. Число всех возможных разбиений -множества А на непустые классы называется числом Белла

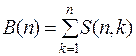. (2.2.6)

 

Для удобства определяют 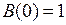, хотя в разбиениях обычно пустые множества не рассматриваются.

 


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.008 сек.)