Прямое произведение множеств

Пусть A и B – два множества. Прямым (декартовым) произведением двух множеств A и B называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит A, а второй принадлежит B.

A B = {(a, b) | a A, b B}.

Пример: точка на плоскости может быть задана упорядоченной парой координат, т.е. двумя точками на координатных осях. Т.о., R² = R R. Метод координат ввел в употребление Рене Декарт (1596 - 1650), отсюда и название – «декартово произведение».

Степенью множества А называется его прямое произведение самого на себя.

Aⁿ =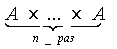

Соответственно, A¹ = A, A² = A A и вообще Aⁿ = A A^n-1.

Теорема: |A B| = |A| |B|.

Доказательство: первый компонент упорядоченной пары можно выбрать |А| способами, второй - |B| способами. Таким образом, всего имеется |A| |B| различных упорядоченных пар.

Следствие: |Aⁿ| = |A|ⁿ.

Поиск по сайту: