 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Правило суммы. Задача: на блюде лежат 5 яблок и 2 груши
Задача: на блюде лежат 5 яблок и 2 груши. Сколькими способами можно выбрать один плод?
Решение: плод можно выбрать семью способами (5+2=7).
Если некоторый элемент a может быть выбран из множества элементов m способами, а другой элемент b может быть выбран n способами, причем любой выбор элемента b отличен от любого выбора элемента a, то выбрать либо a, либо b можно m + n способами.
На языке теории множеств это правило формулируется следующим образом:
Теорема1: если пересечение конечных множеств пусто, то число элементов в их объединении равно сумме чисел элементов множеств А и В.
А  В =
В = 
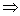 | А
| А  В | = |A| + |B|
В | = |A| + |B|
Разберем случай, когда множества могут иметь непустые пересечения.
Теорема2: для любых конечных множеств верно равенство:
| А  В | = |A| + |B| - | А
В | = |A| + |B| - | А  В |.
В |.
Задача: среди студентов первого курса 30 человек имеют дома компьютер, 35 – учебник по информатике; оказалось, что 10 студентов имеют и компьютер, и учебник по информатике. Сколько студентов на первом курсе?
Решение: пусть множество А составляют студенты, имеющие компьютер, множество В – студенты, имеющие учебник по информатике; по условию задачи:
|A| = 30 |B| = 35 | А  В | = 10 | А
В | = 10 | А  В | =?
В | =?
| А  В | = |A| + |B| - | А
В | = |A| + |B| - | А  В | = 30 + 35 – 10 = 55.
В | = 30 + 35 – 10 = 55.
Поиск по сайту: