 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Сравнение множеств
Множество А содержится во множестве В (множество В включает множество А, множество А является подмножеством В), если каждый элемент множества А является элементом множества В. Обозначение: А 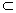 В.
В.
А 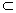 В
В  х
х  А
А  х
х  В.
В.
Два множества называются равными, если они являются подмножествами друг друга. Обозначение: А=В.
А=В  А
А 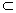 В и В
В и В 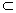 А.
А.
Если непустое множество А является подмножеством В и множества А и В не являются равными, то А является собственным подмножеством В.
Пример: М={4, 6, 8, 10}, К={6, 8}; К 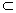 М, М
М, М 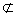 К, М
К, М  К, К – собственное подмножество М.
К, К – собственное подмножество М.
Для множеств существует понятие мощность. Для конечных множеств мощность совпадает с количеством элементов.
Пример: |  |=0, |{
|=0, |{  }|=1, |{1, 2, 3, 4}|=4.
}|=1, |{1, 2, 3, 4}|=4.
Поиск по сайту: