АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

на конечных множествах

Читайте также:
  1. Вычисление конечных и бесконечных сумм и произведений
  2. ЛЕКЦИЯ 4 Общая теория конечных цифровых автоматов с памятью
  3. Метод конечных разностей. Включает следующие этапы
  4. Мощности конечных множеств.
  5. Примерная Модель конечных результатов для поликлиники
  6. Табличный метод структурного синтеза конечных автоматов
  7. Теорема Коши об отношении конечных приращений двух функций
  8. Теорема Лагранжа о конечных приращениях
  9. Технические особенности конечных автоматов
  10. Уравнение теплопроводности в конечных разностях

 

Важнейшим понятием дискретной математики является функциональное отношение, которое есть обобщение понятия функции на произвольные множества.

Опр. 2.3.1. Бинарное отношение называется функциональным, если каждому элементу из А ставится в соответствие единственный элемент из В.

Опр. 2.3.2. Функциональное отношение , для которого для каждого элемента из В найдется хотя бы один элемент из А такой, что называется сюръективным.

 

Замечание. Функциональные отношения часто называют отображениями. Говорят, что отображение R сюръективно, если оно отображает А на В.

 

Частный и чрезвычайно важный пример отображения представляют собой подстановки.

 

Опр. 2.3.3. Подстановкой называется взаимно однозначное отображение множества первых натуральных чисел на себя:

Указанная форма записи, когда элементы в верхней строке упорядочены, называется канонической подстановкой. При этом можно первую строку не выписывать, а указать просто набор вторых чисел . При этом подстановка называется перестановкой. Так как число различных перестановок по существу равно числу различных размещений , то согласно формуле (2.1.4) находим

 

. (2.3.1)

 

Более сложен другой вопрос, связанный с числом различных сюръективных отображений без взаимной однозначности.

Число различных сюръективных отображений из -множества на -множество обозначим как .

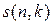Если разбить -множество на непустых классов, то тогда можно ввести взаимно однозначное отображение, действующее из -множества, элементами которого являются классы разбиения, в множество В. Далее используя определение числа Стирлинга второго рода и формулу (2.3.1) для числа перестановок, получим следующий результат.

 

Теорема 2.3.1. Число различных сюръекций и число Стирлинга второго рода связаны соотношением:

 

.


1 | 2 | 3 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)