 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Задача 1. Согласно нулевым столбцам таблиц 1 и 2 имеем следующие исходные данные по инвестиционному проекту Бизнеса:
Согласно нулевым столбцам таблиц 1 и 2 имеем следующие исходные данные по инвестиционному проекту Бизнеса:
К = 800 д.е., Д = 220 д.е./год, Тсл = 12 лет, r = 14%.
1. Определяем бездисконтный срок окупаемости инвестиций:
Т0 = 800/220 = 3.6 года. (1)
В плановой экономике СССР данный показатель являлся основным, характеризующий выгодность государственных инвестиций. На рис.1 (выполнен для условных численных показателей) срок окупаемости (1) представляет абсциссу точки безубыточности t0, лежащей на пересечении линии инвестиций 1 и линейным наращением доходов 2. Действительно, величина Т0 характеризует скорость нарастания доходов во времени, и, если не учитывать инфляцию и вообще понятие процента, по этому показателю можно исчерпывающе судить и целесообразности или нецелесообразности инвестиций. Если бы в плановой экономике попытались оценить суммарный доход от инвестиций за время службы инвестиций, то его отразил бы отрезок (a, d) на рис.1, а суммарный чистый доход – отрезок (b, d). В этой связи одной из основных целей настоящей контрольной работы является обоснование того, что неучет в плановой экономике фактора процента при оценке будущих доходов от инвестиций приводит к совершенно недопустимой ошибке: их выгодность завышается в разы, и по величине ЧДД (см. отрезок (c, b), и по величине ИД.
2. Определение величины суммарного дисконтированного дохода ДД за время действия Тсл инвестиционного оборудования, стоимостью К. В основе практических расчетов лежит следующая формула финансовой математики:
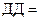
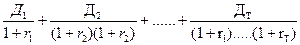 (2)
(2)
где Д i – ежегодный доход в будущем, в год i, от внедренных инвестиций К;
ri – соответствующая процентная ставка, которая обеспечивает доходность вложенных средств (в контексте данного использования ее называют «нормой дисконта»).
Вопрос о прогнозировании средних значений этих величин на период Тсл и об оценке возникающей погрешности от такого усреднения рассмотрен в [1]. Здесь доказано, что даже при значительных разбросах указанных величин вокруг соответствующих средних значений Д и i относительная погрешность итоговой величины (2) находится в пределах 10%, что вполне допустимо для инвестиционных расчетов.
Сказанное позволяет заменить точную формулу (2) упрощенной:
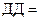
 =
=
= Д[  ]. (3)
]. (3)
В квадратных скобках образовалась убывающая геометрическая прогрессия. Применив формулу для получения суммы ее всех Т членов, приходим к компактной расчетной формуле:
ДД = 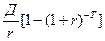 . (4)
. (4)
По формуле (4) на рис.1 построена кривая ДД(t) денежного потока доходов при варьировании аргумента Т от 0 до Тсл .
Срок окупаемости Ток с учетом дисконта отвечает точки пересечения полученной кривой ДД(t) с горизонталью К. Если приравнять (4) величине инвестиций К, то из полученного уравнения нетрудно получить формулу для определения величины Ток :
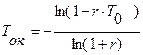 . (5)
. (5)
Остается найти чистый суммарный доход от инвестиций и их рентабельность по формулам:
ЧДД = ДД – К, (6)
ИД = 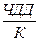 . (7).
. (7).
Продолжим расчет примера. По формуле (5) определяем срок окупаемости с учетом дисконта:
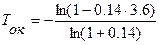 = 5.7 года. (8)
= 5.7 года. (8)
Видим, что учет фактора процента увеличил срок окупаемости почти на 60%.
Рассчитываем показатели общей доходности по формулам (4), (6) и (7):
ДД = 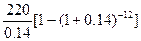 = 1245, (9)
= 1245, (9)
ЧДД = 1245 – 800 = 445, (10)
ИД =  = 0.56. (11)
= 0.56. (11)
Таким образом, инвестиции окупаются почти за 6 лет и через 12 лет принесут чистый доход в размере 0.56 д.е. на 1 д.е. На основе этих данных руководство должно принять решение о целесообразности данных инвестиций.
Заметим, что без учета дисконта рентабельность инвестиций находится на уровне
ИД = 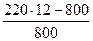 = 2.3, (12)
= 2.3, (12)
что в 4 раза превышает реальную эффективность. Таким образом, линейная модель инвестиций, без учета фактора дисконта, полностью искажает представление об экономической эффективности инвестиций в сторону многократного их увеличения в части их рентабельности – величина ИД. При этом создается искаженное представление и о сроке окупаемости инвестиций – реальный срок превосходит бездисконтный на 40 – 70 процентов.
Анализ формул (4) и (5) показывает, что решающее значение на погрешность линейной модели инвестиций оказывает величина нормы дисконта r, с ее ростом погрешность резко возрастает. Учитывая то, что инфляция в стране еще достаточно долгое время будет значительна, во всяком случае – не менее 5%, пренебрежение в расчетах фактором дисконта недопостимо по причине многократного ошибочного завышения эффективности инвестиций..
Задача 2.
Оценим альтернативную доходность денежных средств К = 800 в портфельной форме их инвестирования (рефинансирования) при среднегодовой ставке i = 4% (табл.3). Срок инвестирования принимаем равным сроку службы прямых инвестиций Т = 12 лет. По формуле наращения капитала по сложным процентам имеем:
К12 = К(1 + i)12 = 800(1+0.04)12 = 1280, (13)
что превышает величину (9), равную 1245. Заметим, что при поквартальном учете процентов (m = 4) наращенный капитал несколько возрастет:
К12 (m) = 800 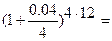 1290. (14)
1290. (14)
По предельной формуле Ирвина Фишера, в идеализированной модели «непрерывного» рефинансирования, имеем:
Ке = 800 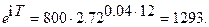 (15)
(15)
Убеждаемся, что при относительно невысоких процентных ставках снижение периода их учета практически не влияет на эффект наращения капитала, и при инвестиционных практических расчетах в равной мере можно пользоваться обеими формулами (13) и (15).
Найдем процентную ставку рефинансирования, которая уравнивает доходность обоих видов инвестирования. Приравнивая (13) и (4), получаем расчетное уравнение:
i = 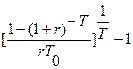 =
= 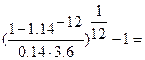 0.038. (16)
0.038. (16)
Поиск по сайту: