АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Математическое описание методов нахождения определенного интеграла

Читайте также:
  1. IDL-описаниеи библиотека типа
  2. II. ОПИСАНИЕ МАССОВОЙ ДУШИ У ЛЕБОНА
  3. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  4. XI. Описание заболевания
  5. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.
  6. Аддитивность интеграла Римана.
  7. Административное принуждение как один из административно – правовых методов. Понятие и особенности административного принуждения.
  8. Алгоритмы методов и их реализация в MS EXCEL
  9. Анализ основных конкурентов (схема и описание)
  10. Аналитические методы при принятии УР, основные аналитические процедуры, признаки классификации методов анализа, классификация по функциональному признаку.
  11. Античное историческое сознание и историописание
  12. Античное историческое сознание и историописание – с. 74-75

1.2.1 Метод Симпсона

Рассмотрим вычисление интеграла

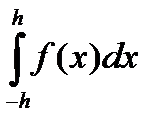
Этот интеграл приближенно заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки

 

Криволинейная трапеция показана на рисунке 2.

Рисунок 7. Криволинейная трапеция.

 

Указанная парабола задается уравнением

 

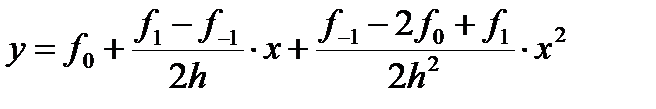
в чем нетрудно убедиться, положив поочередно равным . Отсюда легко находим, интегрируя

 

Таким образом, формула Симпсона, называемая также формулой парабол, имеет вид

 

(5)

Выведем усложненную формулу для приближенного вычисления интеграла на произвольном отрезке .

 

Разобьем отрезок интегрирования на элементарных частей. Длина каждой части

 

 

Тогда границы элементарных отрезков , а значения функции в этих точках , где .

Перепишем каноническую квадратурную формулу Симпсона (5) применительно к отрезку длины .

 

 

Суммируя левую и правую части этого соотношения от до , получаем усложненную квадратурную формулу Симпсона

 

(6)

 

По этой формуле и будем проводить вычисления для заданной функции

 

 


II Практическая часть (2 семестр)

Для функции разработать и протестировать программу, выполняющую:

1. табулирование функции на отрезке [ a; b ] с шагом h;

2. нахождение точек локальных экстремумов;

3. нахождение всех действительных корней уравнения на отрезке [ a; b ], если таковые имеются (решение соответствующего уравнения выполнить с точностью до e =0,0001 одним из численных методов: дихотомии, хорд, касательных не более, чем за 20 итераций.

4. вычисление определенного интеграла f (x) на интервале табулирования [ a; b ] одним из перечисленных методов: правых прямоугольников, средних прямоугольников, левых прямоугольников, трапеций, Симпсона;

5. построение графика заданной функции;

6. построение графика производной заданной функции;

 

F(x) На отрезке Метод для задания № 3 Метод для задания № 4
F(x)= x5-19 • x4 +11 • x3-173 • x2 - 490 • x-500 [-5, 10] дихотомии Симпсона.

 


 

2.1 Табулирование функции на отрезке [ a; b ] с шагом h;

 

Блок-схема

Листинг программы в PascalABC.NET

 

 


 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)