АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Метод хорд (секущих)

Читайте также:
  1. I этап Подготовка к развитию грудобрюшного типа дыхания по традиционной методике
  2. I. ГИМНАСТИКА, ЕЕ ЗАДАЧИ И МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ
  3. I. Методические основы
  4. I. Методические основы оценки эффективности инвестиционных проектов
  5. I. Предмет и метод теоретической экономики
  6. I. Что изучает экономика. Предмет и метод экономики.
  7. II. Метод упреждающего вписывания
  8. II. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
  9. II. Методы непрямого остеосинтеза.
  10. II. Проблема источника и метода познания.
  11. II. Рыночные методы.
  12. II. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА ДИСЦИПЛИНЫ

Метод хорд – это итерационный численный метод приближённого нахождения корня уравнения.

ПРАВИЛО ПРОПОРЦИОНАЛЬНЫХ ЧАСТЕЙ

Если промежуток [a, b] достаточно мал, то с известным приближением можно считать, что – при измерении x в его пределах – приращение функции f(x) пропорционально приращению аргумента. Обозначая через корень функции, имеем, в частности,

= ,

 

откуда, с учетом того, что

 

f( =0, =a-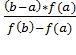

 

Таким образом, за приближенное значение корня здесь принимается число x1 = a- 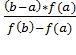. Это выражение, очевидно, можно представить и в такой форме: x1 = b- . Изложенное правило получения приближенного значения корня и называется правилом пропорциональности частей. (см.[1]).

 

ГЕОМЕТРИЧЕСКОЕ ОПИСАНИЕ МЕТОДА ХОРД

 

Правило пропорциональности частей допускает простое геометрическое истолкование. Рассмотрим рисунок:

 

Рисунок 5.

Заменим дугу MM / кривой – хордой MM / . Уравнение последней может быть написано, например в виде:

y-f(a) = 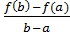(x-a). (3)

 

Наше правило, по существу, сводится к тому, что вместо точки А пересечения кривой с осью x определяется точкаD пересечения с осью x этой хорды.

Действительно, полагая в (3) уравнении y=0, а для абсциссы x1 точки D получаем именно выражение вида:

 

x1 = b-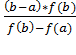

 

В связи с этим, правило пропорциональных частей называют также методом хорд. Ну а теперь обратимся к исследованию вопроса о положении точки x1 по отношению к корню . Непосредственно ясно, что точка x1 лежит между a и b, но с какой стороны от ? Выясним это.

Так в случаях I и II (III и IV) мы имеем дело с выпуклой вниз (вверх) функцией, то кривая MM / лежит под (над) хордой MM / , то есть

f(x) f(a)+ 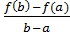(x-a) (a<x<b) (4)

 

Полагая здесь x=x1 , непосредственно получаем f(x1) 0, так что f(x1) всегда имеет знак противоположный знаку f // (x). Отсюда, наконец, заключаем, что в случаях I и IV значение x1 лежит между a и , в случаях же II и III – между и b.

Ограничиваясь случаями I и IV, применим снова наше правило, на этот раз к промежутку [х1, b], заменяя в (2) а на x1 получим новое приближенное значение корня :

 

x2=x1 - ,

 

содержащееся, по доказанному, между х1 и Этот процесс можно продолжать неопределенно и построить последовательность все возрастающих приближенных значений

a<x1<x2<…<xn<xn+1<…< .

 

При этом любые два последовательных значения хп и хп+1 связаны формулой, аналогичной (2),

xn+1=xn - (5)

 

Покажем, что, с возрастанием п, хп В самом деле, монотонно возрастающая, но ограниченная (например, числом ) переменная хп должна стремиться к некоторому конечному пределу . Если перейти к пределу в равенстве (5), используя при этом непрерывность функции f(x), то получим, что

 

, откуда f( )=0.


Так как другихкорней уравнения (1), кроме , в промежутке [а, b] нет, то = *).

 

Рисунок 6.

Рисунок 6. иллюстрирует постепенное приближение точек D1, D2,... • пересечения последовательных хорд с осью х к искомой точке А. Легко понять, что в случаях II или III повторное применениеправила приведет к последовательности убывающих приближенных значений b>x1>x2>… >xn>xn+1>…> стремящихся к корню справа. Таким образом, во всех случаях, применив достаточное число раз указанное выше правило, можно вычислить корень с любой степенью точности. При этом, впрочем, остается открытым вопрос, как оценить точность уже вычисленного приближенного значения хп.

Для решения его применим к разности f(xn)- f( ) формулу конечных приращений:

f(xn) =f(xn)-f( ) =(xn- ) f / (c) ( ) c xn).

Отсюда xn- ;

 

если обозначить через т наименьшее значение | f / (x) | в рассматриваемом промежутке (которое можно раз навсегда вычислить наперед), то получим оценку:

| xn- | . (6)

 

Так по самой величине f(xn) оказывается возможным судить о близости хп к корню!


 


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.742 сек.)