Метод дихотомии

Контрольная работа

по дисциплине «Информационные технологии»

на тему «Исследование функции»

Выполнил: студент группы

ТАМП (МТФ)-14-1бз

М.Е.Климов

Проверил: преподаватель П.Н. Килина

Пермь, 2015

Содержание

I Теоретическая часть. 3

1.1 Математическое описание методов нахождения корней уравнения. 3

1.1.1 Метод дихотомии. 3

1.1.2 Метод Ньютона (касательных) 4

1.1.3 Метод хорд (секущих) 7

1.2 Математическое описание методов нахождения определенного интеграла. 11

1.2.1 Метод левых/средних/правых прямоугольников/ метод трапеций/метод Симпсона – 1 метод по заданию из общей таблицы вариантов. 11

II Практическая часть (2 семестр) 13

2.1 Табулирование функции на отрезке [ a; b ] с шагом h; 14

2.2 Нахождение точек локальных экстремумов. 15

2.3 Нахождение всех действительных корней уравнения методом дихотомии /хорд /касательных 16

2.4 Вычисление определенного интеграла методом правых прямоугольников/ средних прямоугольников/ левых прямоугольников/ трапеций/ Симпсона. 17

Список литературы.. 18

I Теоретическая часть

Математическое описание методов нахождения корней уравнения

Метод дихотомии

Метод дихотомии также называют методом половинного деления. Этот метод решения уравнений отличается тем, что для него не требуется выполнения условия, что первая и вторая производная сохраняют знак на интервале [a, b]. Метод половинного деления сходится для любых непрерывных функций f(x) в том числе недифференцируемых.

Разделим отрезок [a, b] пополам точкой 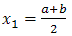. Если (что практически наиболее вероятно), то возможны два случая: либо f(x) меняет знак на отрезке [a, x1] (Рисунок. 1), либо на отрезке [x1, b] (Рисунок. 2).

Рисунок 1 На отрезке [a, x1}

Рисунок 2 На отрезке [x1, b]

Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

Поиск по сайту: