Стоячие волны

Пусть скалярная величина 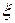зависит от координат рассматриваемой точки 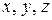и времени 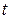следующим образом:

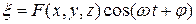, (3.10)

где 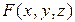– некоторая однозначная функция, 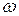и 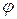– постоянные. Это значит, что величина 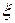во всех точках пространства совершает гармоническое колебание с одинаковой частотой и фазой, но амплитуда колебания различна для различных точек пространства. Такое явление называется стоячей волной. Волну (6.6) для того, чтобы подчеркнуть ее отличие от стоячей волны, называют бегущей волной.

Для частного случая плоской стоячей волны амплитуда зависит только от одной координаты, скажем :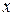

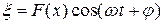. (3.11)

Интерес представляет случай, когда 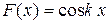, т. е.

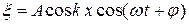, (3.12)

где 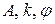- постоянные, т. е. когда распределение амплитуды в пространстве синусоидально. Такая стоячая волна называется синусоидальной стоячей волной.

Докажем, что суперпозиция двух бегущих плоских синусоидальных волн одинаковой амплитуды и частоты, распространяющихся в противоположных направлениях, есть стоячая плоская синусоидальная волна.

В самом деле, пусть 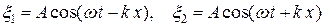. Тогда .

Воспользуемся формулой ,

. (3.13)

Это – уравнение стоячей волны.

В точках среды, где

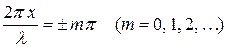, (3.14)

амплитуда результирующей стоячей волны достигает максимального значения, равного 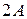. Она вдвое больше амплитуды каждой из бегущих волн. Эти точки называются пучностями стоячей волны.

В точках среды, где

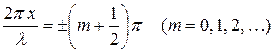, (3.15)

амплитуда колебаний падает до нуля. Эти точки все время остаются в покое. Они называются узлами стоячей волны.

Из формул (3.14) и (3.15) следует, что соседние узлы и пучности отстоят на расстоянии полуволны друг от друга.

Таким образом, основное отличие стоячей волны от бегущей заключается в том, что все точки стоячей волны между соседними узлами колеблются с разными амплитудами, но в одной фазе, в то время как все точки бегущей волны совершают колебания с одинаковой амплитудой, но с разными фазами.

Поиск по сайту: