АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Плоская монохроматическая волна. Волновой вектор

Читайте также:
  1. Волновой дуализм де Бройля
  2. Волновой пакет. Возможные скорости(4 штуки). Скорость переноса энергии. Связь групповой скорости с фазовой. Дисперсия упругих волн.
  3. Вопрос 60 Корпускулярно – волновой дуализм
  4. Вторая волна.
  5. Вторая революционная волна. апрель-август 1905 г.
  6. Если вы привязаны к форме, если вы отождествляете себя с формой, если вы ощущаете себя формой, то вы навлекаете на себя неприятности. Вы океан, а не волна.
  7. Корпускулярно-волновой дуализм
  8. Корпускулярно-волновой дуализм. Длина волны де Бройля. Квантование электронных орбит атома в модели де Бройля. Соотношения неопределенностей.
  9. Линейные операции с геометрическими векторами. Координаты геометрического вектора. Радиуса-вектор.
  10. Механические волны. Плоская волна
  11. Первая волна.
  12. Плоская волна

 

Особый интерес представляет частный случай, когда функция синусоидальна:

. (3.6)

В каждой точке пространства, где значение 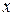фиксировано, величина совершает гармоническое колебание. Его амплитуда равна , а круговая частота равна 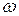. Обе эти величины одинаковы для всех 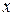. Фаза колебания равна 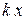. Она различна для различных 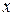и пропорциональна расстоянию от плоскости . Коэффициент пропорциональности 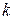между фазой и расстоянием называется волновым числом. При положительных значениях выражение (3.6) описывает волну, распространяющуюся
в сторону возрастающих 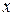(слева направо), а выражение

(3.6а)

– волну, распространяющуюся в сторону убывающих значений 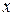(справа налево).

Моментальный снимок волны (3.6) – график зависимости при фиксированном значении 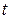– есть синусоида в пространстве. Например, в момент времени .

Пространственный период 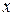такой, что при любом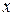 , называют длиной волны. Длина волны равна тому пути, который проходит волна за один период колебаний. Длина волны связана
с волновым числом соотношением (ср. соотношение, связывающее 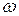и ): , откуда

. (3.7)

Физический смысл волнового вектора: величина 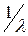дает число волн, укладывающихся в (густоту волн), следовательно, 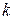– это число «кусочков» волны, укладывающихся в . Каждый «кусочек» в раз меньше длины волны. В оптике часто называют волновым вектором величину .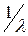

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Фазовая скорость волны – это скорость, с которой распространяется фаза колебания, равна:

, (3.8)

где - период колебания. Формула (6.6) может быть также записана в виде:

. (3.9)

Из такой записи сразу видно, что колебание в плоскости 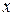воспроизводит колебания в плоскости с опозданием на секунд.


1 | 2 | 3 | 4 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)