АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Волновое уравнение

Читайте также:
  1. Волновое сопротивление
  2. Волновое сопротивление
  3. Волновое уравнение для упругих волн и его общее решение.
  4. Волновое уравнение для электромагнитных волн
  5. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  6. Волновое уравнение. Фазовая скорость упругих волн.
  7. Дифференциальное волновое уравнение. Скорость распространения волн
  8. Получить уравнение плоской бегущей гармонической волны для произвольной декартовой системы координат и вывести из него волновое уравнение.
  9. Трехмерное волновое уравнение

Тема № 12.1 ВОЛНОВЫЕ ПРОЦЕССЫ

 

1. Волны. Волновое уравнение

2. Интерференция и дифракция волн

 

Волны. Волновое уравнение

Понятие волны.

 

Как происходит распространение колебаний – передача воздействия от источника к приемнику. Как доходят до нашего уха колебания давления воздуха, возникающие около звучащего камертона? Каким образом свет, испускаемый звездами, достигает нашего глаза?

Для рассмотрения подобного рода вопросов необходимо ввести новое физическое понятие – волны. В физике волнами или волной называют всякое изменяющееся со временем пространственное чередование максимумов и минимумовлюбой физической величины, например плотности вещества, напряженности электрического поля, температуры.

Волной часто называют также всякое явление, при котором в пространстве происходит распространение кратковременного электрического или механического «толчка». Таким образом, понятие «волна» охватывает обширный круг явлений.

Замечание. К огда речь идет о волнах на поверхности воды, волной (в единственном числе) называют обычно совокупность одногогорба
иодной смежной с ним впадины. Когда говорят (также в единственном числе) «звуковая (или электромагнитная) волна такой-то частоты», всегда имеют в виду бесконечную вереницу «горбов» и «впадин».

Волновое уравнение.

 

Рассмотрим произвольную функцию

(3.1)

от аргумента . Продифференцируем ее дважды по времени :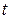

,

. (3.2)

Здесь штрих означает дифференцирование по аргументу . Теперь продифференцируем нашу функцию дважды по координате :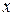

. (3.3)

Сравнивая (3.2) и (3.3), убеждаемся, что функция (3.1) удовлетворяет уравнению

или , (3.4)

в котором – фазовая скорость волны. Легко видеть, что этому же уравнению удовлетворяет произвольная функция аргумента :

(3.5)

а также сумма функций вида (3.1) и (3.5).

Дифференциальное уравнение в частных производных (3.4) называется волновым уравнением. При положительных значениях функции (3.1) и (3.5) изображают плоские волны, распространяющиеся, не деформируясь, со скоростью в сторону соответственно возрастающих или убывающих значений .


1 | 2 | 3 | 4 |

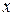Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)