 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ. Механические колебания- это движения, которые точно или приблизительно повторяются через определенный промежуток времени
Механические колебания- это движения, которые точно или приблизительно повторяются через определенный промежуток времени.
Свободные механические колебания рассматриваются на примерах колебаний математического и пружинного маятников.
Математический маятник – материальная точка, совершающая колебания на невесомой нерастяжимой нити.
Пружинный маятник – тело, совершающее колебания на пружине под действием силы упругости.
ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЮЩИЕ КОЛЕБАНИЯ:
1. СМЕЩЕНИЕ 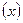 -отклонение тела от положения равновесия.
-отклонение тела от положения равновесия.

2. АМПЛИТУДА  -максимальное по модулю отклонение тела от положения равновесия.
-максимальное по модулю отклонение тела от положения равновесия.
3.ПЕРИОД (Т)-промежуток времени, за который тело совершает одно полное колебание.
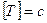
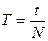 , где t-время, в течение которого совершено N колебаний.
, где t-время, в течение которого совершено N колебаний.
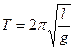 - формула для вычисления периода колебаний математического маятника.
- формула для вычисления периода колебаний математического маятника.
Если маятник совершает колебания в условиях при которых увеличивается сила натяжения нити, например, маятник движется с ускорением, направленным вертикально вверх, на маятник, кроме силы тяжести, действует, направленная вниз электрическая сила и т.п., то период колебаний математического маятника вычисляется по формуле: 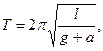 где
где  сила, приводящая к увеличению силы натяжения нити.
сила, приводящая к увеличению силы натяжения нити.
Если маятник совершает колебания в условиях при которых уменьшается сила натяжения нити, например, маятник движется с ускорением, направленным вертикально вниз, на маятник, кроме силы тяжести, действует, направленная вверх электрическая сила и т.п., то период колебаний математического маятника вычисляется по формуле:  где
где  сила, приводящая к увеличению силы натяжения нити.
сила, приводящая к увеличению силы натяжения нити.
 - формула для вычисления периода колебаний пружинного маятника.
- формула для вычисления периода колебаний пружинного маятника.
4. ЧАСТОТА (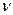 )- число колебаний N, совершаемых телом за единицу времени.
)- число колебаний N, совершаемых телом за единицу времени.
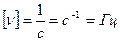 (герц)
(герц)
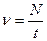
5. СВЯЗЬ ПЕРИОДА И ЧАСТОТЫ: 
6. ЦИКЛИЧЕСКАЯ ЧАСТОТА 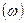 - число колебаний за 2
- число колебаний за 2  секунд.
секунд.


Различают свободные и вынужденные колебания. Свободные колебания происходят под действием внутренних, направленных к положению равновесия сил, возникающих после выведения колебательной системы из положения равновесия. Вынужденные колебания происходят под действием внешней, периодически изменяющейся, направленной к положению равновесия силы.
Если тело одновременно совершает свободные и вынужденные колебания, то возможен резонанс. Резонанс - это резкое возрастание амплитуды колебаний при
совпадении частоты собственных колебаний с частотой вынуждающей силы.
Гармонические колебания – это колебания, происходящие по закону синуса или косинуса. Если при  , то колебания происходят по закону синуса; уравнение для
, то колебания происходят по закону синуса; уравнение для  имеет вид:
имеет вид:  Если при
Если при 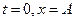 , то колебания происходят по закону косинуса; уравнение для
, то колебания происходят по закону косинуса; уравнение для  имеет вид:
имеет вид: 
В записанных формулах 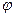 - фаза колебаний.
- фаза колебаний. 
 где
где  - начальная фаза колебаний.
- начальная фаза колебаний.
Каждому значению времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах, например:
если 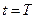 , то
, то  ; если
; если 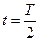 , то
, то  .
.

При гармонических колебаниях периодически изменяются координата, скорость, ускорение, кинетическая и потенциальная энергия тела.

| 
| 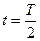
| |||
| Математический маятник | 
| 
| 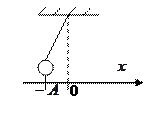
| ||
| Пружинный маятник | 
| 
|

| ||
| Координата | 
| ||||
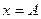
| 
| 
| |||
| Скорость |  , где , где  - амплитуда
скорости. - амплитуда
скорости.
| ||||
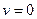
| 
| 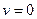
| |||
| Ускорение | 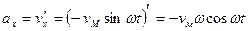 ,где ,где  -
амплитуда ускорения
Если колебания совершает математический маятник, то данные равенства относятся к тангенциальному ускорению, т.к. траекторией в данном случае является дуга окружности, то колеблющееся тело обладает еще центростремительным ускорением и полное ускорение ни в одной из точек не равно нулю. -
амплитуда ускорения
Если колебания совершает математический маятник, то данные равенства относятся к тангенциальному ускорению, т.к. траекторией в данном случае является дуга окружности, то колеблющееся тело обладает еще центростремительным ускорением и полное ускорение ни в одной из точек не равно нулю.
| ||||

| 
| 
| |||
| Кинетическая энергия | 
| 
| 
| ||
| Потенциальная энергия | 
|  , если нулевой потенциальный уровень совпадает с положением равновесия , если нулевой потенциальный уровень совпадает с положением равновесия
| 
| ||
| Полная энергия | 
| ||||

| 
| 
|
Содержание
Поиск по сайту:
