Блок-схема решения задач имитационного моделирования

Активный эксперимент позволяет получить статистические модели процессов формирования в технологической системе параметров состояния поверхностного слоя или их эксплуатационных свойств от условий обработки, а также эксплуатационных характеристик обрабатываемых поверхностей от параметров их качества, то есть зависимости типа «режимы обработки – параметры качества поверхности», «режимы обработки – эксплуатационные показатели поверхности», «параметры качества поверхности – эксплуатационные показатели поверхности». На основе таких моделей исследуется параметрическая надёжность технологических систем по обеспечению качества поверхностей и эксплуатационных свойств соединений.

Экспериментально установлено, что модели функций технологических процессов с достаточной для практических целей точностью можно представить в виде полиномиальной (аддитивной) модели

Y_i = b ₀ + b ₁ X ₁ + … + b _i X _i + … + b_k X_k,

где Y_i – i -й параметр состояния поверхностного слоя или эксплуатационных свойств соединения после обработки; X_i – i -й фактор технологического процесса; b₀, b_i – истинные значения коэффициентов регрессии.

Аддитивные модели этого вида строятся из предположения линейной связи между функцией Y_i и аргументами X_i. Такие случаи в технике и технологии встречаются достаточно редко. Чаще приходится иметь дело с нелинейной зависимостью оцениваемых пара­метров относительно рассматриваемых факторов. В таких случаях для упрощения полу­чения моделей исходные данные подвергают преобразованиям, глав­ное назначение которых состоит в линеаризации рассматриваемых зависимос­тей по оцениваемым параметрам. В частности, одним из таких мето­дов является логарифмирование исходных данных, которое позволяет получить модель процесса в виде функции Кобба-Дугласа (мультипликативная модель)

.

Логарифмирование приводит к линейной зависимости

ln Y_i = ln b ₀ + b ₁ × ln X ₁ + … + b_k × ln X_k.

Эти модели являются приближённой имитацией формирования показателей процесса в технологической системе. Одним из их недостатков является неудовлетворительная точность и отсутствие адекватного отклика на изменяющиеся условия протекания моделируемого процесса.

Если же в этих моделях случайными являются один или несколько факторов X_i, то для оценок М { Y_i } и S ²{ Y_i }, аналитические выражения найти не удаётся. В этом случае их оп­ределение связано с обработкой массива, данных Y_iN, полученных в результате машинного эксперимента (МЭ) путём N прогонов соответствующих имитационных моделей по схеме Монте-Карло (рис.).

В качестве исходных данных используются результаты построения имита­ционных моделей, конструкторские и технологические ограничения.

В общем случае в число исходных данных входят:

1) имитационная модель для параметра Y = f (b ₀, b_i, X_i);

2) имитационная модель скорости изменения параметра Y в процессе функционирования технологической системы g = f (x ₀, x_i, X_i);

Рис. Блок-схема расчёта показателей надёжности ТС

по показателям качества методом Монте-Карло

3) математические ожидания и средние квадратические отклонения ко­эффициентов и случайных факторов обработки М { b_i }, S { b_i }, М { x_i }, S { x_i }, М { X_i }, S { X_i };

4) допустимые пределы изменения параметра Y, заложенные в конструк­торской документации, и время безотказного функционирования тех­нологической системы, то есть Y_max, Y_min, T;

5) допустимые пределы варьирования технологических факторов обра­ботки Х_{i max}, Х_{i min};

6) доверительная вероятность a и допустимые абсолютные ошибки оп­ределения оценок М { Y }, S ²{ Y } (величины а и d).

Определяются номинальные значения технологических факторов X_i, обеспечивающие получение требуемого значения параметра Y ₀. При этом в соответствующих имитаци­онных моделях используются коэффициенты b_i = M { b_i }. При рас­чёте условий обработки, обеспечивающих получение величины Y в заданном интервале [ Y_min, Y_max ], обязательно анализируется выполнение технических тре­бований по точности размеров и погрешности формы обрабатываемой детали.

В дальнейшем осуществляется тактическое планирование, связанное с эффективным использованием машинных ресурсов, обеспечением точности и достоверности (что особенно важно) результатов машинного эксперимента, формирующего массив данных по i-му параметру качества КПС или ЭС Y_i.

Важным является вопрос о выборе числа прогонов модели N в процессе машинного эксперимента. Число прогонов N должно удовлетворять заданной точности оценки величин М { Y_i } и S ²{ Y_i } по результатам машинных экспериментов.

Для генерации случайных величин X_i, b_0j, b_ij, x _{0 i}, x_ij в процессе машинного эксперимента исполь­зуется датчик псевдослучайных чисел. Сначала генерируются равно­мерно распределённые случайные числа в интервале (0, 1), а затем формируется нормально распределённое случайное число с парамет­рами M { b_i } = b_i и S { b_i }.

После расчёта N значений параметра Y_i проверяются статистические гипотезы, и оцениваются параметры распределения.

По полученным данным 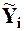и строятся гистограммы распределений, включающие интервалов, и проверяются гипоте­зы о законе распределения (рассматриваются распределение Вейбулла, нормальное и логарифмически-нормальное распределения) с помощью критерия c ².

Если 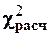£ 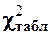для данного уровня значимости a и числа степеней свободы, то нет оснований отвергать нулевую гипотезу, и принимается соответствующий ей закон распределения.

Затем, используя оцениваются вероятности выполнения заданий ТС по i -му параметру КПС или ПЭС. Эти вероятности характеризуют параметрическую надёжность ТС по обеспечению данного параметра в заданных границах.

Такая процедура повторяется для всех регламентируемых параметров и рассчитывается вероятность выполнения задания ТС в соответствии с по всем m обеспечиваемым параметрам качества:

P (t) = min { P ₁(t),..., P_i (t), …, P_m (t)}.

При исследовании показателей надёжности технологической системы методом имитаци­онного моделирования на статистических моделях следует чётко представлять, что моделируется только «прошлое», то есть при этом использу­ются данные, полученные экспериментально на этапе построения ими­тационных моделей. Следовательно, чтобы прогноз, сделанный на основе имитационного моделирования, оправдался, необходимо пред­положить, что основная форма распределения параметров ТС во времени остаётся неизменной и её особенно­сти, относящиеся к определенному промежутку времени, будут повто­ряться. Такие допущения следует принять для нормально функцио­нирующего технологического процесса. На случаи внезапных отказов ТС результаты предложенного подхода не распространяются.

Вопросы для самопроверки

1. В каких случаях проводится имитационное моделирование и что оно собой представляет?

2. Какими моделями удовлетворительно описываются функции технологических систем?

3. какие блоки входят в систему расчета показателей качества ТС методом Монте-Карло?

4. Что моделируется в процессе имитационного моделирования системы: ее «прошлое» или «будущее» и почему?

5. Перечислите основные этапы оценки параметрической надёжности технологических систем методом Монте-Карло.

6. Что такое «машинный эксперимент»? Как его организовать?

7. Как обеспечиваются заданные законы распределения параметров имитационной модели в процессе машинного эксперимента по схеме Монте-Карло?

Рекомендуемая литература.

1. Аверченков, В.И. Основы математического моделирования технических систем: учеб. пособие / В.И. Аверченков, В.П. Федоров., М.Л. Хейфец – Брянск: Изд-во БГТУ, 2004.

2. Вентцель, Е.С. Исследование операций / Е.С. Вентцель. – М.:Наука, Гл. ред. физ.-мат. лит., 1998.

3. Шеннон, Р. Имитационное моделирование систем – искусство и наука / Р. Шеннон. –М.: Мир, 1978.

Лекция 6. (Окончание раздела 4) «Роль и место машинных экспериментов в процессе моделирования объектов машиностроения» (2 часа)

План лекции:

6.1. Планирование машинных экспериментов. Моделирование по схеме Монте-Карло.

6.2. Анализ результатов и принятие решений.

Планирование машинных экспериментов. Моделирование по схеме Монте-Карло

Эксперимент должен быть информативен, то есть давать всю нужную информацию, которой следует быть полной, точной, достоверной. Но она должна быть получена приемлемым способом. Это означает, что способ должен удовлетворять экономическим, временным и, возможно, другим ограничениям. Такое противоречие разрешается с помощью рационального (оптимального) планирования эксперимента.

Теория планирования эксперимента сложилась в шестидесятые годы двадцатого века благодаря работам выдающегося английского математика, биолога, статистика Рональда Айлмера Фишера (1890-1962 гг.). Одно из первых отечественных изданий: Федоров В. В. Теория оптимального эксперимента. 1971 г. Несколько позже сложилась теория и практика планирования имитационных экспериментов.

Будем считать, что эксперимент состоит из наблюдений, а каждое наблюдение - из прогонов (реализаций) модели.

Для организации экспериментов наиболее важно следующее.

1. Простота повторений условий эксперимента.

2. Возможность управления экспериментом, включая его прерывание и возобновление.

3. Легкость изменения условий проведения эксперимента (воздействий внешней среды).

4. Исключение корреляции между последовательностями данных, снимаемых в процессе эксперимента с моделью.

5. Определением временного интервала исследования модели ().

Компьютерный эксперимент с имитационной моделью обладает преимуществами перед натурным экспериментом по всем этим позициям.

Компьютерный эксперимент представляет собой процесс использования модели с целью получения и анализа интересующей исследователя информации о свойствах моделируемой системы.

Эксперимент требует затрат труда и времени и, следовательно, финансовых затрат. Чем больше мы хотим получить информации от эксперимента, тем он дороже.

Средством достижения приемлемого компромисса между максимумом информации и минимумом затрат ресурсов является план эксперимента.

План эксперимента определяет:

· объем вычислений на компьютере;

· порядок проведения вычислений на компьютере;

· способы накопления и статистической обработки результатов моделирования.

Планирование экспериментов имеет следующие цели:

· сокращение общего времени моделирования при соблюдении требований к точности и достоверности результатов;

· увеличение информативности каждого наблюдения;

· создание структурной основы процесса исследования.

Таким образом, план эксперимента на компьютере представляет собой метод получения с помощью эксперимента необходимой информации.

Весь комплекс действий по планированию эксперимента разделяют на две самостоятельные функциональные части:

· стратегическое планирование;

· тактическое планирование.

Стратегическое планирование - разработка условий проведения эксперимента, определение режимов, обеспечивающих наибольшую информативность эксперимента.

Тактическое планирование обеспечивает достижение заданных точности и достоверности результатов.

Формирование стратегического плана выполняется в так называемом факторном пространстве. Факторное пространство - это множество внешних и внутренних параметров, значения которых исследователь может контролировать в ходе подготовки и проведения эксперимента.

Математические методы планирования экспериментов основаны на так называемом кибернетическом представлении процесса проведения эксперимента

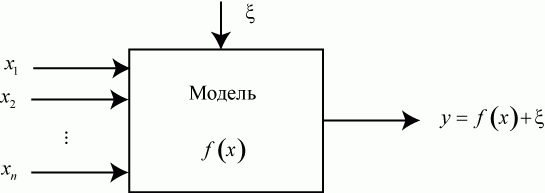
Рис. Кибернетическое представление эксперимента

– входные переменные, факторы;

– выходная переменная (реакция, отклик);

– ошибка, помеха, вызываемая наличием случайных факторов;

– оператор, моделирующий действие реальной системы, определяющий зависимость выходной переменной 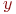от факторов

Иначе: - модель процесса, протекающего в системе.

Первой проблемой, решаемой при стратегическом планировании, является выбор отклика (реакции), то есть определение, какие величины нужно измерять во время эксперимента, чтобы получить искомые ответы. Естественно, выбор отклика зависит от цели исследования.

Второй проблемой стратегического планирования является выбор (определение) существенных факторов и их сочетаний, влияющих на работу моделируемого объекта. Факторами могут быть питающие напряжения, температура, влажность, ритмичность поставок комплектующих и многое другое. Обычно число факторов велико и чем меньше мы знакомы с моделируемой системой, тем большее, нам кажется, число их влияет на работу системы. В теории систем приводится так называемый принцип Парето:

· 20% факторов определяют 80% свойств системы;

· 80% факторов определяют 20% свойств системы. Следовательно, надо уметь выделять существенные факторы.

Факторы могут быть количественными и (или) качественными.

Количественные факторы - это те, значения которых числа. Например, интенсивности входных потоков и потоков обслуживания, емкость буфера, число каналов в СМО, доля брака при изготовлении деталей и др.

Качественные факторы - дисциплины обслуживания (LIFO, FIFO и др.) в СМО, «белая сборка», «желтая сборка» радиоэлектронной аппаратуры, квалификация персонала и т.п.

Фактор должен быть управляемым. Управляемость фактора - это возможность установки и поддержания значения фактора постоянным или изменяющимся в соответствии с планом эксперимента. Возможны и неуправляемые факторы, например, влияние внешней среды.

К совокупности воздействующих факторов предъявляются два основных требования:

· совместимость;

· независимость.

Совместимость факторов означает, что все комбинации значений факторов осуществимы.

Независимость факторов определяет возможность установления значения фактора на любом уровне независимо от уровней других факторов.

Третьей проблемой стратегического планирования является выбор значений каждого фактора, называемых уровнями фактора.Число уровней может быть два, три и более.

Для удобства и, следовательно, удешевления эксперимента число уровней следует выбирать поменьше, но достаточное для удовлетворения точности и достоверности эксперимента. Минимальное число уровней - два.

С точки зрения удобства планирования эксперимента целесообразно устанавливать одинаковое число уровней у всех факторов. Такое планирование называют симметричным.

Основной задачей тактического планирования является обеспечение результатам компьютерного эксперимента заданных точности и достоверности.

Основная идея статистического имитационного моделирования (метода Монте-Карло) заключается в многократном расчёте определяемого параметра (или параметров) по известным зависимостям, описывающим процесс потери работоспособности, причём для случайных аргументов, входящих в расчётные формулы, перебираются их наиболее вероятные значения в соответствии с известными законами распределения. Результатом каждого статистического испытания выявляется одна из реализаций случайного процесса, совокупность которых позволяет оценить его тип и основные параметры. Большой объём вычислений при реализации метода Монте-Карло требует, как правило, достаточно мощных средств вычислительной техники.

Процедура метода Монте-Карло состоит из нескольких этапов:

1. На первом этапе в зависимости от необходимой точности определения характеристик надёжности выбирается необходимое число реализаций N.

2. Из заданного диапазона изменения каждого аргумента по известным законам распределения f (Z_i) случайным образом (с использованием таблицы или генератора случайных чисел) выбирается по N значений каждого аргумента

3. Из полученных значений аргументов Z_i случайным образом выбираются N наборов значений (в каждом наборе по одному значению каждого аргумента Z_i). Для каждого из наборов значений рассчитывается N значений определяющего параметра X. По выборке из N значений параметра X Î { X ₁, X ₂, …, X_j, …, X_N } методами математической статистики строятся гистограмма частоты попадания значения параметра X в k -й интервал N_k / N, кривая плотности распределения f (X) и интегральная кривая функции распределения F (X) параметра X. Полученные кривые f (X) и F (X) аппроксимируются какой-либо функцией распределения (если это необходимо).

При действии случайных факторов наиболее приемлемым для моделирования надёжности является метод статистических испытаний.

Блок-схема реализации метода Монте-Карло для моделирования прочностной надёжности представлена на рисунке.

Рис. Блок-схема реализации метода Монте-Карло

при расчёте вероятности безотказной работы элемента

по параметру прочности

Поиск по сайту: