 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Моделирование технических систем на основе алгебры логики
Моделирование процессов и объектов машиностроения предполагает, наряду с численными методами, широкое использование математических операций с высказываниями, которые имеют свою специфику и свои законы, рассматриваемые алгеброй логики. Модели алгебры и исчисления высказываний рассматривают связи между высказываниями, которые воспринимаются через выражающие их предложения соответствующего предметного языка.
Овладению им способствует усвоение понятий о простых и составных высказываниях, элементарной алгебры логики. Для спешного решения задач, возникающих при этом, необходимо знание порядка моделирования логических высказываний и технических систем на основе синтеза комбинационных схем. Выражение значительной части знаний, относящихся как к математике, так и к естественному разговорному языку, возможно на основе логической системы – исчисления предикатов первого порядка.
В соответствии с теоретико-множественным подходом в алгебре высказываний в качестве элементов множества выступают простые высказывания, операции над которыми и являются содержанием этой алгебры.
Простое высказывание – каждое утверждение, которое в определенных условиях времени и места может быть истинным или ложным.
Высказывания рассматриваются по отношению к элементам некоторого универсального множества 
. Отдельные элементы этого множества будут обладать различными свойствами и в соответствии с этим могут образовывать различные группы, представляющие собой подмножества множества . Так, если – множество инструмента, то его подмножествами могут быть: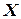 
– множество резцов; 
– множество сверл; 
– множество зенкеров и т.д.
Высказывания будем обозначать строчными латинскими буквами и приписывать каждому из них численные значения: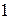 
(если высказывание истинно) и 
(если оно ложно). Пусть 
означает высказывание «это резец». Его численные значения будут равны:
Логической операцией над простыми высказываниями называется построение из них нового составного высказывания. Совокупность таких логических операций получила название алгебры высказываний, или булевой алгебры.
Приняты три способа изображения булевых функций:
1. Формула, указывающая в явном виде последовательность логических операций, производимых над высказываниями 
,и имеющая вид соотношения.
2. Таблица, указывающая значения истинности составного высказывания 
в зависимости от значений истинности исходных высказываний. В левой части таблицы перечисляются все возможные комбинации значений истинности исходных высказываний , а в правой части – значения истинности составного высказывания . Если имеется N исходных высказываний, то число строк таблицы будет равно 
.
3. Логическая схема, представляющая собой условное графическое обозначение логической операции.
В вычислительной технике и автоматике отдельные высказывания обычно представляются в виде сигналов, имеющих два уровня (0 и 1), или в виде устройств, которые могут принимать два состояния (реле, триггер, транзистор и др). Состояние сигналов в ЭВМ или приборов в системах автоматики определяют значения истинности соответствующих высказываний.
При таком подходе логическая схема представляет собой преобразователь сигналов, который можно использовать для целей управления различными процессами.
Логические операции можно интерпретировать с помощью диаграмм Эйлера – Венна, напоминающих диаграммы геометрической интерпретации тождеств алгебры множеств.
Вопросы для самопроверки.
1. Определение графа и способы его представления.
2. Какие задачи могут решаться с помощью теории графа?
3. Как математически могут представляться графы?
4. Как формируются простые высказывания в алгебре логики?
5. Как изображаются булевы функции?
6. Какие логические операции используются в элементарной алгебре высказываний?
Рекомендуемая литература
1. Аверченков, В.И. Основы математического моделирования технических систем: учеб. пособие / В.И. Аверченков, В.П. Федоров., М.Л. Хейфец – Брянск: Изд-во БГТУ, 2004
2. Коршунов, Ю.М. Математические основы кибернетики: учебн. пособие для вузов / Ю.М. Коршунов. –М.: Энергия, 1987.
3. Кузин, Л.Т. Основы кибернетики: В 2 т. Т.2. Основы кибернетических моделей: учебн. пособие для вузов / Л.Т. Кузин. – М.: «Энергия», 1973.
Раздел 3: «Методы построения моделей и идентификации исследуемых процессов, явлений и объектов в машиностроении» (4 часа)
Лекция 3. «Методы построения моделей и идентификации исследуемых процессов, явлений и объектов» (1 час)
План лекции:
3.3. Физико-статистическое моделирование формирования выходных параметров технологических процессов в машиностроении.
3.4. Основы кибернетического моделирования.
3.3. Физико-статистическое моделирование формирования выходных параметров технологических процессов в машиностроении.
В соответствии с ГОСТ 27.004-85, технологическая система – это совокупность функционально взаимосвязанных средств технологического оснащения, предметов производства и исполнителей для выполнения в регламентированных условиях производства заданных технологических процессов или операций. К предметам производства относятся материал, заготовка, полуфабрикат и изделие, находящиеся в соответствии с выполняемым технологическим процессом в стадии хранения, транспортирования, формообразования, обработки, сборки, ремонта, контроля и испытаний.
Для современных технологических систем характерна совокупность взаимосвязанных потоков энергии, материалов и информации, действующая как единое целое, в котором осуществляется определённая последовательность процессов.
Параметрическая надёжность ТС на уровне технологического процесса в работе определяется как его свойство обеспечивать изготовление продукции в заданном объёме, сохраняя во времени установленные требования к её качеству. Причём надёжность технологических систем должна оцениваться только по тем параметрам и показателям качества изделия, уровень которых зависит от технологии и изготовления.
Особенности формирования выходных параметров технологического процесса не обеспечивают равенство вероятности Pi (t) произведению вероятностей Piq (t) для каждой операции.
Параметрический отказ ТС – это отказ технологической системы, при котором сохраняется её функционирование, но происходит выход значений одного или нескольких параметров технологического процесса за пределы, установленные в нормативно-технической и (или) конструкторской и технологической документации. Здесь имеются в виду параметры, относящиеся непосредственно к технологической системе.
В этом плане одним из критериев отказа ТС является выход одного из регламентируемых показателей качества детали, указанных в конструкторской и технологической документации, за допустимые пределы. Одним из важнейших показателей безотказности ТС по i -у параметру качества является вероятность выполнения задания, которая для обеспечения одновременно всех m параметров определена:
P { Ei 1 £ y 1(t) £ Es 1; Ei 2 £ y 2(t) £ Es 2; …; Eim £ ym (t) £ Esm } = P (t).
Здесь Eij, Esj 1 – соответственно нижнее и верхнее предельные отклонения для i -го параметра, установленные НТД; yj (t) – значения j-го параметра в момент t. При этом наработка Т может измеряться в единицах времени, циклах функционирования или в единицах изготовленной продукции.
Вероятность выполнения задания ТС по j -му параметру определяется на основе выражения
P { Eij £ yj (t) £ Esj } £ Pj (t).
В основу оценки показателей надёжности ТС по параметрам качества продукции методом статистического моделирования может быть положен функционально-статистический подход, который базируется на построении модели технологического процесса, связывающей условия обработки, в том числе случайные воздействия, и параметры качества обработанной детали. Такие модели, адекватно описывая конкретные условия технологического процесса, могут противоречить физическим представлениям о механизме происходящих процессов.
Гораздо предпочтительней концепция нового физико-статистического подхода, которая заключается в том, что структура модели технологического процесса формируется на основе физико-технологического анализа причинно-следственных связей факторов обработки и внешней среды, а выходные параметры определяются статистическими методами. Такой подход может быть принят в качестве основного при постановке и решении большинства задач содержательной части системной методологии исследования надёжности ТС.
Для построения моделей и исследования надёжности ТС целесообразно применять метод имитационного моделирования, так как он характеризуется высокой эффективностью при сравнительно небольших материальных затратах. Построение и анализ моделей ТС методом имитационного моделирования базируется на основе математико-статистического подхода к анализу сложных систем и предполагает использование метода статистических испытаний (Монте-Карло). Имитационное моделирование ТС включает методологию построения системных моделей, методы алгоритмизации объектов, методы и средства построения программных реализаций имитаторов, планирование организации и выполнение на ЭВМ экспериментов с имитационными моделями, машинную обработку данных и анализ результатов. Таким образом, для оценки показателей надёжности ТС по параметрам качества обрабатываемых деталей необходимо:
1) построить статистические модели функции ТС вида (181)одним из методов, выбранным по результатам априорной деформации;
2) используя соответствующие алгоритмы и программное обеспечение, реализовать машинные эксперименты в выбранной области факторного пространства по схеме Монте-Карло и проанализировать с целью оценки вероятностных характеристик выходных величин моделируемой ТС;
3) спрогнозировать показатели надёжности технологического обеспечения КПС или ПЭС обрабатываемой детали для данной ТС.
Таким образом, в схеме определения показателей надёжности ТС, отвечающей такой методологии можно отметить наличие двух этапов исследования: построение и анализ имитационных моделей для ТС (группа А) и расчёт показателей надёжности ТС (группа В).
Построение формальных имитационных моделей наиболее эффективно проводить с помощью активного эксперимента, применяя известные методы корреляционно-регрессионного анализа и теории планирования эксперимента.
Поиск по сайту: