Введение. Классификация моделей по типам, свойствам и назначению. Методы моделирования сложных систем

Т Е З И С Ы Л Е К Ц И Й

по дисциплине

«Математическое моделирование в машиностроении»

Раздел 1. «Модели процессов, явлений и объектов в машиностроении и методы их построения» (2 часа)

Лекция 1. «Модели процессов, явлений и объектов в машиностроении и методы их построения» (2 часа)

План лекции:

1.1. Введение. Классификация моделей по типам, свойствам и назначению. Методы моделирования сложных систем.

1.2. Основные принципы построения математических моделей.

1.3. Средства математического моделирования технических объектов и обеспечение

Введение. Классификация моделей по типам, свойствам и назначению. Методы моделирования сложных систем.

Известно, что моделирование (в широком смысле) является основным методом исследований во всех областях знаний и научно-обоснованным методом оценок характеристик сложных систем, используемых в различных сферах инженерной деятельности, в частности в машиностроении.

Методологическая основа моделирования состоит в упорядочении получения и обработки информации об объектах, которые существуют вне нашего сознания и взаимодействуют между собой и внешней средой. Объект (лат. objectum – предмет) – все то, на что может быть направлена человеческая деятельность.

В математическом моделировании большую роль играют следующие категории:

Гипотеза – определенное предсказание, основывающееся на небольшом количестве опытных данных, наблюдений, догадках. В ходе специально поставленного эксперимента может быть проведена быстрая и полная проверка выдвигаемых гипотез.

Аналогия – суждение о каком-либо частном сходстве объектов, которое может быть существенным и несущественным. Причем понятия существенности и несущественности, сходства или различия объектов условны и относительны. Существенность сходства или различия зависит от уровня абстрагирования и определяется конечной целью проводимого исследования. Аналогия имеет большое значение в качестве метода суждения при формулировании и проверке правильности гипотез. Модель – (лат. modulus – мера) – это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала. Иными словами, модели – удобные для исследования логические схемы, построенные на основе гипотез и аналогий, упрощающие рассуждения и логические построения или позволяющие проводить эксперименты, уточняющие природу явлений.

Известно много определений модели. Остановимся на некоторых из них:

Модель – это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта.

Это определение можно заменить более кратким эквивалентом:

Модель есть системное отображение оригинала, на основании которого могут быть введены следующие дополнения:

· моделирование – замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели путем проведения экспериментов над последней;

· теория моделирования – теория замещения одних объектов (оригиналов) другими объектами (моделями).

Одной из важнейших характеристик в определении модели является ее адекватность, которая зависит от цели моделирования и принятых критериев. Модель адекватна объекту, если результаты моделирования подтверждаются и могут служить основой для прогнозирования поведения технических объектов или процессов, протекающих в реальных исследуемых системах, с регламентируемой точностью, удовлетворяющей выбранному критерию адекватности.

При проектировании как сложной технической системы в целом, так и ее подсистем необходимо выполнить внешнее проектирование (макропроектирование) и внутреннее (микропроектирование). На указанных стадиях рассматриваются различные цели, что приводит к существенному различию используемых при этом методов и средств моделирования. На стадии макропроектирования должна быть разработана обобщенная модель процесса функционирования сложной системы, позволяющая разработчику получить ответы на вопросы об эффективности различных стратегий управления объектом при его взаимодействии с внешней средой. Стадию внешнего проектирования можно разбить на анализ и синтез. При анализе изучают объект управления, строят модель воздействий внешней среды, определяют критерии оценки эффективности, имеющиеся ресурсы, необходимые ограничения. Конечная цель стадии анализа – построение модели объекта управления для оценки его характеристик. При синтезе на этапе внешнего проектирования решаются задачи выбора стратегии управления на основе модели объекта моделирования, т.е. сложной системы.

На стадии микропроектирования разрабатывают модели с целью создания эффективных подсистем. Причем используемые методы и средства моделирования зависят от того, какие конкретно обеспечивающие подсистемы разрабатываются: информационные, математические, технические, программные и т.д.

Современные методы и средства моделирования технических систем неразрывно связаны с новыми достижениями в различных областях науки и техники, а в особенности с процессом совершенствования ЭВМ, сфера эксплуатации которых распространяется на все отрасли человеческой практики и стимулирует развитие новых теоретических и прикладных направлений, в том числе и в машиностроении.

Из методов моделирования можно выделить аналитические и имитационные:

· аналитические методы к исследованию системы (исторически первый) предусматривают использование ЭВМ в качестве вычислителя по аналитическим зависимостям. Анализ характеристик процессов при таком методе связан со значительными трудностями: возникает необходимость существенного упрощения модели на этапе их построения или в процессе работы с ней, что может привести к получению недостоверных результатов;

· имитационные методы основаны на оценке характеристик больших технических систем, представляемых в виде имитационных моделей, реализованных на современных ЭВМ с высоким быстродействием и большим объемом оперативной памяти;

· «чисто машинные» методы –новые методы решения задач исследования больших систем на основе реализации имитационных экспериментов с их моделями.

Однако при всем совершенстве применяемой вычислительной техники нельзя игнорировать тот факт, что в основу любой модели положено предварительное изучение явлений, лежащих в объекте-оригинале. Успех моделирования технической системы, как и любой другой, зависит в конечном счете от того, насколько детально изучены реальные явления, в объекте-оригинале.

В зависимости от специфики исследуемых объектов в ряде случаев эффективным оказывается моделирование на аналоговых вычислительных машинах (АВМ). При этом надо иметь в виду, что АВМ значительно уступают ЭВМ по точности и логическим возможностям, но по быстродействию, схемной простоте реализации, сопрягаемости с датчиками внешней информации АВМ превосходят ЭВМ или по крайней мере не уступают им.

Для сложных динамических объектов наиболее перспективным является моделирование на базе гибридных (аналого-цифровых) вычислительных комплексов. Такие комплексы реализуют преимущества цифрового и аналогового моделирования и позволяют наиболее эффективно использовать ресурсы ЭВМ и АВМ в составе единого комплекса. При использовании гибридных моделирующих комплексов упрощаются вопросы взаимодействия с датчиками, установленными на реальных объектах, что позволяет, в свою очередь, проводить комбинированное моделирование с использованием аналого-цифровой части модели и натурной части объекта.

В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может быть лишь при замене объекта другим, точно таким же. Как указывалось раньше, при моделировании стремятся к тому, чтобы модель достаточно хорошо отражала исследуемую сторону функционирования объекта, так как в этом случае абсолютного подобия нет. В соответствии с поставленной целью моделирования построенные модели различают по типу, своему назначению, а значит, и по выполняемым функциям, структуре и т.д.

Укрупненная классификация моделей по типу и свойствам, которая дает достаточно четкое представление об их главных отличительных чертах, показана на рисунке.

Классификация моделей по типам

Рассмотрим их краткие характеристики и главные отличительные особенности.

1. Материальные (реже – вещественные, действующие, наглядные) модели – это некоторые материальные объекты или совокупность объектов, отражающие в той или иной степени свойства объекта моделирования. В зависимости от полноты и способа отражения этих свойств материальные модели подразделяются на три основных типа:

· геометрические модели – представляют некоторый объект, геометрически подобный своему оригиналу, и дают внешнее представление об оригинале. Выполняются как в натуральную величину (модели отливок и др.), так и в уменьшенном масштабе (модель нового автомобиля, демонстрационная модель детали или агрегата машины и т.д.).

· физические модели – отражают подобие между оригиналом и моделью не только с точки зрения их формы и геометрических соотношений, но и с позиций происходящих основных физических процессов. Необходимо помнить и всегда иметь в виду, что физически подобными называются явления в геометрически подобных системах, в процессе функционирования которых отношения характеризующих их физических величин в сходственных точках составляют постоянную величину. При физическом моделировании модель и объект моделирования всегда должны иметь одинаковую физическую природу. При изменении геометрических параметров при переходе от объекта-оригинала к модели должны соответственно изменяться и другие физические параметры, являющиеся входными или возбуждающими воздействиями.

Предметно-математические модели – предполагается лишь тождественность математического описания процессов в оригинале и модели (требование тождественности их физической природы снимается), хотя эти процессы и могут развиваться на совершенно различной материальной основе. В этом случае предметно-математическая модель представляет материальную систему, в которой происходят иные физические процессы, чем в оригинале, но и те, и другие могут быть описаны одинаковыми или подобными математическими выражениями.

2. Идеальные модели (абстрактные концептуальные) включают модели двух типов:

· мысленные (умозрительные, интуитивные) – существуют в мыслях человека, воображаются человеком.

· логико-математические (формальные, знаковые, математи­ческие) – представляют собой воплощение мысленных моделей в форму различных математических выражений (системы уравнений или неравенств с буквенными или численными коэффициентами, логические выражения, таблицы, матрицы, схемы, графики и др.) и других способов логического и математического описания исследуемых явлений и процессов. В принципе это не что иное, как математические модели.

В группе математических моделей, в свою очередь, выделяются подгруппы:

А. Модели прямой аналогии, в которых каждой физической величине оригинала сопоставляется в модели величина другого рода, изменяющаяся в пространстве и во времени сходным образом.

Б. Структурные или операционные модели, в которых математическое описание оригинала воспроизводят в виде совокупности отдельных операций, выполняемых соответствующими блоками.

В. Цифровые модели, в которых те же операции выполняются в цифровом виде, обычно последовательно одна за другой в общем процессоре.

Г. Функциональные модели, в которых воспроизводится только поведение, функция оригинала, но не его устройство, так что по описанию модель может быть не подобна натуре.

В машиностроении в последнее время широко используются относительно новые типы математических моделей:

· физико-аналитические модели – представляют собой аналитические зависимости между входными факторами и выходными параметрами технологических и иных систем, полученные на основе анализа реально протекающих физических процессов и их аналитических описаний.

Наиболее ярким примером могут служить модели формирования параметров качества поверхностного слоя и процессов контактирования шероховатых поверхностей.

· физико-статистические модели – представляют собой зависимости между входными параметрами технологических и иных систем, полученные статистическими методами (методами планирования эксперимента, множественного корреляционно- регрессионного анализа и др.), но факторы, включённые в исследование, имеют четкий физический смысл и являются реальными технологическими переменными. Такие модели не следует относить к типу эмпирических, так как они строятся на базе активного, а не пассивного эксперимента, т.е. с использованием кибернетического подхода, и не представляют собой процесс сглаживания результатов пассивных наблюдений, который осуществляется подбором подходящего уравнения, включающего то или иное число независимых переменных, не несущих на себе никакой нагрузки с точки зрения физики протекающих в реальной системе процессов. Такие модели строятся в том случае, когда физику протекающих процессов аналитически описать не представляется возможным. Однако на их основе возможно с достаточной надёжностью прогнозировать параметры качества поверхностного слоя (КПС) обрабатываемых деталей и др., формируемые в ходе обработки при заданных условиях, а также осуществлять процесс управления технологической системой, обеспечивающий получение параметров качества обработки в допустимых пределах с заданной надёжностью.

В общем случае математические модели связывают входные (независимые) переменные 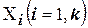исследуемого процесса, называемые входными факторами, или воздействиями, с выходными (зависимыми) характеристиками , которые обычно именуют функциями отклика (например, в технологических системах это параметры точности обработки, качества поверхностного слоя; энергозатраты, производительность и др.). Такие уравнения связи имеют вид:

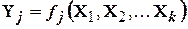
Модели, отображающие случайный (стохастический) характер параметров и факторов системы, называются статистическими, или стохастическими в отличие от детерминированных, не учитывающих вероятностных характеристик процессов.

По мере уменьшения величины параметров 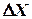и 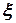уравнение приближается по структуре к уравнению, описывающему детерминированные системы.

Обычно детерминированные модели, представляющие собой систему уравнений, удается составить только в тех случаях, когда о процессах в описываемой системе имеются ясные физические представления и эти представления можно формализировать. В таких случаях говорят, что система представляет собой «белый ящик» – объект с известной структурой и функциями.

Однако получаемая таким образом модель может оказаться громоздкой, а ее информационное обеспечение весьма трудоемким. Поэтому часто используют статистические модели для описания детерминированных систем. В таких случаях рассматривают систему как «черный ящик» с неизвестной структурой, в котором доступны для изучения только контролируемые входные параметры 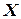и измеримые выходные характеристики . Получив таблицу соответствий { 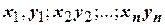}, принимают их за случайную выборку из генеральной статистической совокупности { }. Полученная статистическая модель при соответствующей интерпретации результатов позволяет раскрыть механизм, сделать «белыми» некоторые части устройства и функционирования «черного ящика».

Схемы моделей производственных систем при наличии в них детерминированных (а) и стохастических (б) процессов

Детерминированные модели могут также использоваться для описания стохастических систем, если объектом изучения являются их усредненные характеристики. Таким образом, статистические модели – это более широкий класс моделей, включающих детерминированные модели как предельный частный случай, в котором выходные параметры однозначно определяются входными переменными .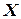

Если доказано подобие натурных и моделирующих процессов, то можно говорить об адекватности моделей.

В зависимости от характера и пространственной структуры описываемых систем различаются модели с распределенными и сосредоточенными параметрами. В связи с различной интенсивностью моделируемых процессов во времени различают статические модели, описывающие установившиеся процессы вблизи состояния равновесия; стационарные модели, характеризуемые постоянством основных параметров во времени; динамические модели систем, в которых входной переменной процесса является время.

В зависимости от конкретного вида применяемого математического аппарата различают модели матричные, сетевые, дифференциальные, интегральные, алгоритмические, программные и др.

Кроме изложенной классификации моделей по типу, существует часто используемый вид классификации моделей по назначению. В этом плане их можно разбить на следующие:

1. Информационные (описательные), используемые в качестве обучающих или советующих систем, для изучения взаимного влияния факторов на выходные параметры, установления границ, в пределах которых достигается рациональный режим работы системы и т.д.

2. Оптимизационные, используемые для поиска оптимальных условий протекания процесса в системе. В качестве оптимизационных могут применяться информационные модели, дополненные блоком оценки результата на основании целевой функции, с учетом налагаемых ограничений на изменение входных и выходных переменных.

3. Управления (регулирования) процессом, используемые для воздействия на систему в реальном масштабе времени с целью компенсации нежелательных случайных возмущений и смещения системы в направлении экстремального значения целевой функции. Такая модель может служить компонентом системы автоматического управления (регулирования).

4. Эвристические, используемые для получения новых знаний и изучения механизма процессов на основе сопоставления результатов моделирования и натурных измерений, выдвижения и проверки новых гипотез о структуре взаимосвязей между факторами, введения дополнительных факторов в модель и т.д.

Поиск по сайту: